Download.vn Học tập Lớp 10 Lớp 12 Thi THPT Quốc Gia
Bạn đang đọc: Tư duy dồn biến trong bất đẳng thức
Tư duy dồn biến trong bất đẳng thức Tài liệu ôn tập môn Toán lớp 10
Giới thiệu Tải về Bình luận
- 1
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Nhằm đem đến cho các bạn học sinh có thêm nhiều tài liệu học tập môn Toán chuyên đề Bất đẳng thức, Download.vn giới thiệu tài liệu Tư duy dồn biến trong bất đẳng thức.
Đây là tài liệu hữu ích, gồm 13 bài toán bất đẳng thức được xử lý bằng phương pháp dồn biến. Tài liệu có đáp án chi tiết kèm theo. Hy vọng với tài liệu này các bạn có thêm nhiều tài liệu tham khảo củng cố kiến thức đạt được kết quả cao trong các bài kiểm tra, bài thi THPT Quốc gia sắp tới.
Tư duy dồn biến trong bất đẳng thức
 I. Giới thiệu cơ bản về bất đẳng thức Cauchy (AM – GM): Bất đẳng thức Cauchy cho hai số:a b ab a babab a b22 , , 0,,2 . Đẳng thức xảy ra khi ab. Bất đẳng thức Cauchy cho ba số:a b c a bc a b ca b cabc a b c333 , , , 0, , , 03 . Đẳng thức xảy ra khi a b c Bất đẳng thức Cauchy tổng quát cho nsố không âm:nn n nnnnna a a n a a a a a aa a aa a a a a an1 2 1 2 1 2121 2 1 2… … , , ,… 0…… , , ,… 0 . Đẳng thức xảy ra khi na a … a12 II. Các hệ quả của bất đẳng thức Cauchy (AM – GM):a b ab, a,b222 . Đẳng thức xảy ra khi ab.a b ab, a,b222 . Đẳng thức xảy ra khi ab. abab22, a,b. Đẳng thức xảy ra khi ab.a b c abc, a,b,c3 3 330 . Đẳng thức xảy ra khi a b c. a b cabc33, a,b,c 0. Đẳng thức xảy ra khi a b c. ab bc ca a b c a b c a b c22 2 23 3 , , , . Đẳng thức xảy ra khi a b c. a b ab a b a b33, , 0 . Đẳng thức xảy ra khi ab. aba b a bba22, , 0 . Đẳng thức xảy ra khi ab.IV. Sử dụng bất đẳng thức AM – GM đưa về biến cần tìm:Bài 1: Cho các số thực ,xythỏa mãnxy0. Tìm giá trị nhỏ nhất của: P x y x y3323 .Bài 2: Cho các số thực ,xydương. Tìm giá trị nhỏ nhất của biểu thức: P x yxy x y22188 .Bài 3: Cho các số thực dương xy,. Tìm giá trị nhỏ nhất của biểu thức: Pxyx y x y3 3 3 311924H HỌC TOÁN – CHIẾN THẮNG 3 CÂU PHÂN LOẠIGiáo viên: Đoàn Trí Dũng – Hà Hữu Hải BÀI 6: AM – GM Dồn biến
I. Giới thiệu cơ bản về bất đẳng thức Cauchy (AM – GM): Bất đẳng thức Cauchy cho hai số:a b ab a babab a b22 , , 0,,2 . Đẳng thức xảy ra khi ab. Bất đẳng thức Cauchy cho ba số:a b c a bc a b ca b cabc a b c333 , , , 0, , , 03 . Đẳng thức xảy ra khi a b c Bất đẳng thức Cauchy tổng quát cho nsố không âm:nn n nnnnna a a n a a a a a aa a aa a a a a an1 2 1 2 1 2121 2 1 2… … , , ,… 0…… , , ,… 0 . Đẳng thức xảy ra khi na a … a12 II. Các hệ quả của bất đẳng thức Cauchy (AM – GM):a b ab, a,b222 . Đẳng thức xảy ra khi ab.a b ab, a,b222 . Đẳng thức xảy ra khi ab. abab22, a,b. Đẳng thức xảy ra khi ab.a b c abc, a,b,c3 3 330 . Đẳng thức xảy ra khi a b c. a b cabc33, a,b,c 0. Đẳng thức xảy ra khi a b c. ab bc ca a b c a b c a b c22 2 23 3 , , , . Đẳng thức xảy ra khi a b c. a b ab a b a b33, , 0 . Đẳng thức xảy ra khi ab. aba b a bba22, , 0 . Đẳng thức xảy ra khi ab.IV. Sử dụng bất đẳng thức AM – GM đưa về biến cần tìm:Bài 1: Cho các số thực ,xythỏa mãnxy0. Tìm giá trị nhỏ nhất của: P x y x y3323 .Bài 2: Cho các số thực ,xydương. Tìm giá trị nhỏ nhất của biểu thức: P x yxy x y22188 .Bài 3: Cho các số thực dương xy,. Tìm giá trị nhỏ nhất của biểu thức: Pxyx y x y3 3 3 311924H HỌC TOÁN – CHIẾN THẮNG 3 CÂU PHÂN LOẠIGiáo viên: Đoàn Trí Dũng – Hà Hữu Hải BÀI 6: AM – GM Dồn biến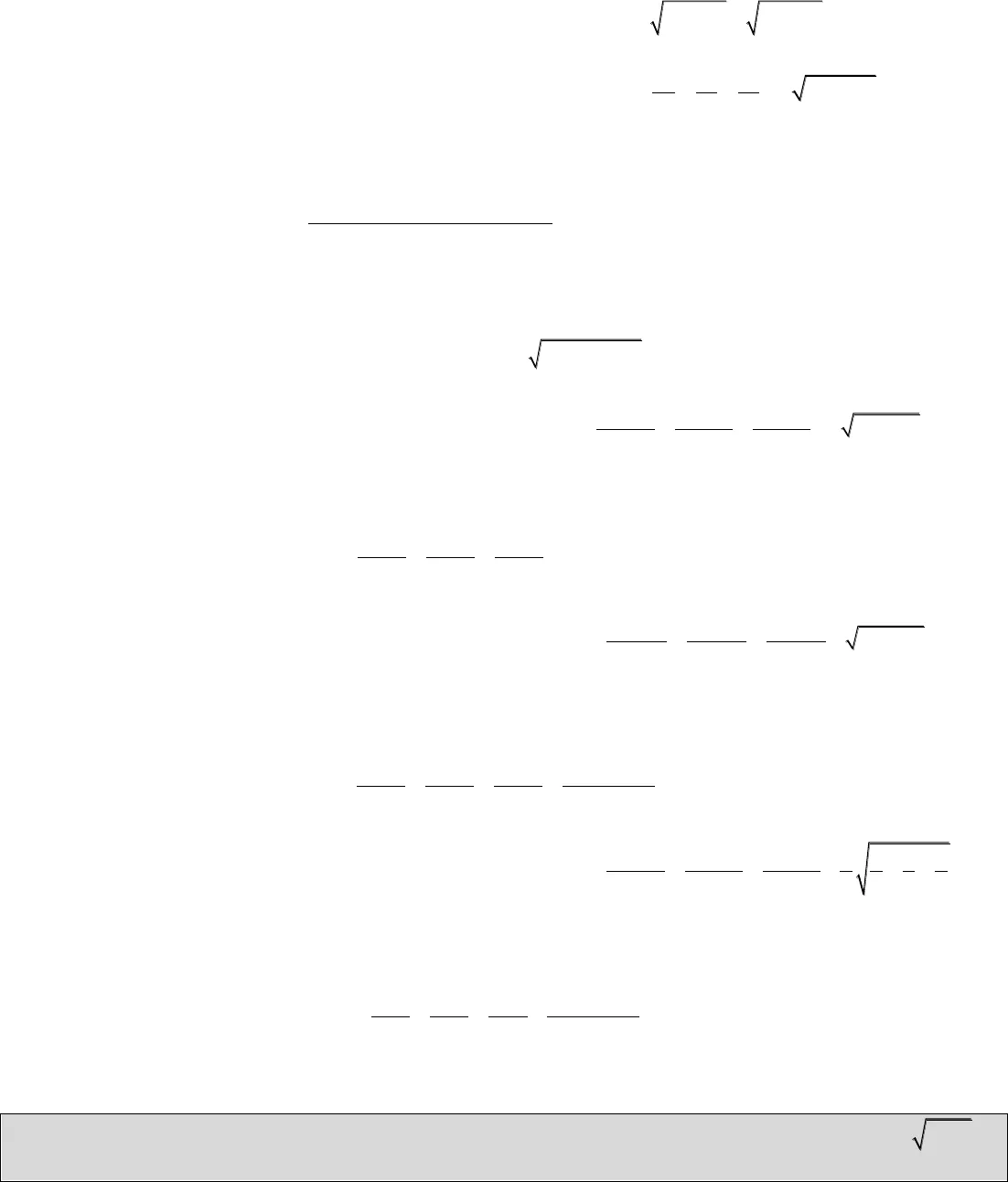 Bài 4: Cho ,,a b cthỏa mãnc a c b c0, , . Tìm giá trị lớn nhất của: 222 P c a c c b c a bBài 5: Cho các số thực a b c, , 0. Tìm giá trị nhỏ nhất của biểu thức: 2 ab bc caP a b cc a bBài 6: Cho a b c,,độ dài 3 cạnh một tam giác. Tìm giá trị nhỏ nhất của biểu thức: 2 2 211 P a b c abca b c b c a c a b.Bài 7: Cho các số thực dương xyz,,thỏa mãnxyz 1. Tìm giá trị nhỏ nhất của biểu thức:4 4 433 P x y y z z x xy yz zxBài 8: Cho các số thực a b c,,dương. Tìm giá trị nhỏ nhất của: 2 2 244 a bc b ca c abP a b cb c c a a bBài 9: Cho các số thực dương a b c,,thỏa mãn3 a b c. Tìm giá trị nhỏ nhất của biểu thức: 32 2 21 1 1 a b cP a b cb c a.Bài 10: Cho các số thực dương a b c,,. Tìm giá trị nhỏ nhất của: 3 3 32 2 2 2 2 2 abcP a b ca b b c c aBài 11: Cho các số thực dương a b c,,thỏa mãn điều kiện 1abc. Tìm giá trị nhỏ nhất của biểu thức: 32 2 21 1 1541 1 1 a b ca b cPb c aBài 12: Cho các số thực dương a b c,,. Tìm giá trị nhỏ nhất của: 3 3 33 3 3 32 a b cPa b cb ab c bc a caBài 13: Cho các số thực dương a b c,,thỏa mãnabc 1. Tìm giá trị lớn nhất của biểu thức: 21 1 11 1 1 6 a b ca b cPb c aĐÁP ÁN Bài 1: Cho các số thực ,xythỏa mãnxy0. Tìm giá trị nhỏ nhất của biểu thức: P x y x y3323 .Phân tích Biến cần đưa về: xy. Chiều đánh giá cần có: P . Chiều cần đánh giá cần tìm: x y f x y33 .
Bài 4: Cho ,,a b cthỏa mãnc a c b c0, , . Tìm giá trị lớn nhất của: 222 P c a c c b c a bBài 5: Cho các số thực a b c, , 0. Tìm giá trị nhỏ nhất của biểu thức: 2 ab bc caP a b cc a bBài 6: Cho a b c,,độ dài 3 cạnh một tam giác. Tìm giá trị nhỏ nhất của biểu thức: 2 2 211 P a b c abca b c b c a c a b.Bài 7: Cho các số thực dương xyz,,thỏa mãnxyz 1. Tìm giá trị nhỏ nhất của biểu thức:4 4 433 P x y y z z x xy yz zxBài 8: Cho các số thực a b c,,dương. Tìm giá trị nhỏ nhất của: 2 2 244 a bc b ca c abP a b cb c c a a bBài 9: Cho các số thực dương a b c,,thỏa mãn3 a b c. Tìm giá trị nhỏ nhất của biểu thức: 32 2 21 1 1 a b cP a b cb c a.Bài 10: Cho các số thực dương a b c,,. Tìm giá trị nhỏ nhất của: 3 3 32 2 2 2 2 2 abcP a b ca b b c c aBài 11: Cho các số thực dương a b c,,thỏa mãn điều kiện 1abc. Tìm giá trị nhỏ nhất của biểu thức: 32 2 21 1 1541 1 1 a b ca b cPb c aBài 12: Cho các số thực dương a b c,,. Tìm giá trị nhỏ nhất của: 3 3 33 3 3 32 a b cPa b cb ab c bc a caBài 13: Cho các số thực dương a b c,,thỏa mãnabc 1. Tìm giá trị lớn nhất của biểu thức: 21 1 11 1 1 6 a b ca b cPb c aĐÁP ÁN Bài 1: Cho các số thực ,xythỏa mãnxy0. Tìm giá trị nhỏ nhất của biểu thức: P x y x y3323 .Phân tích Biến cần đưa về: xy. Chiều đánh giá cần có: P . Chiều cần đánh giá cần tìm: x y f x y33 .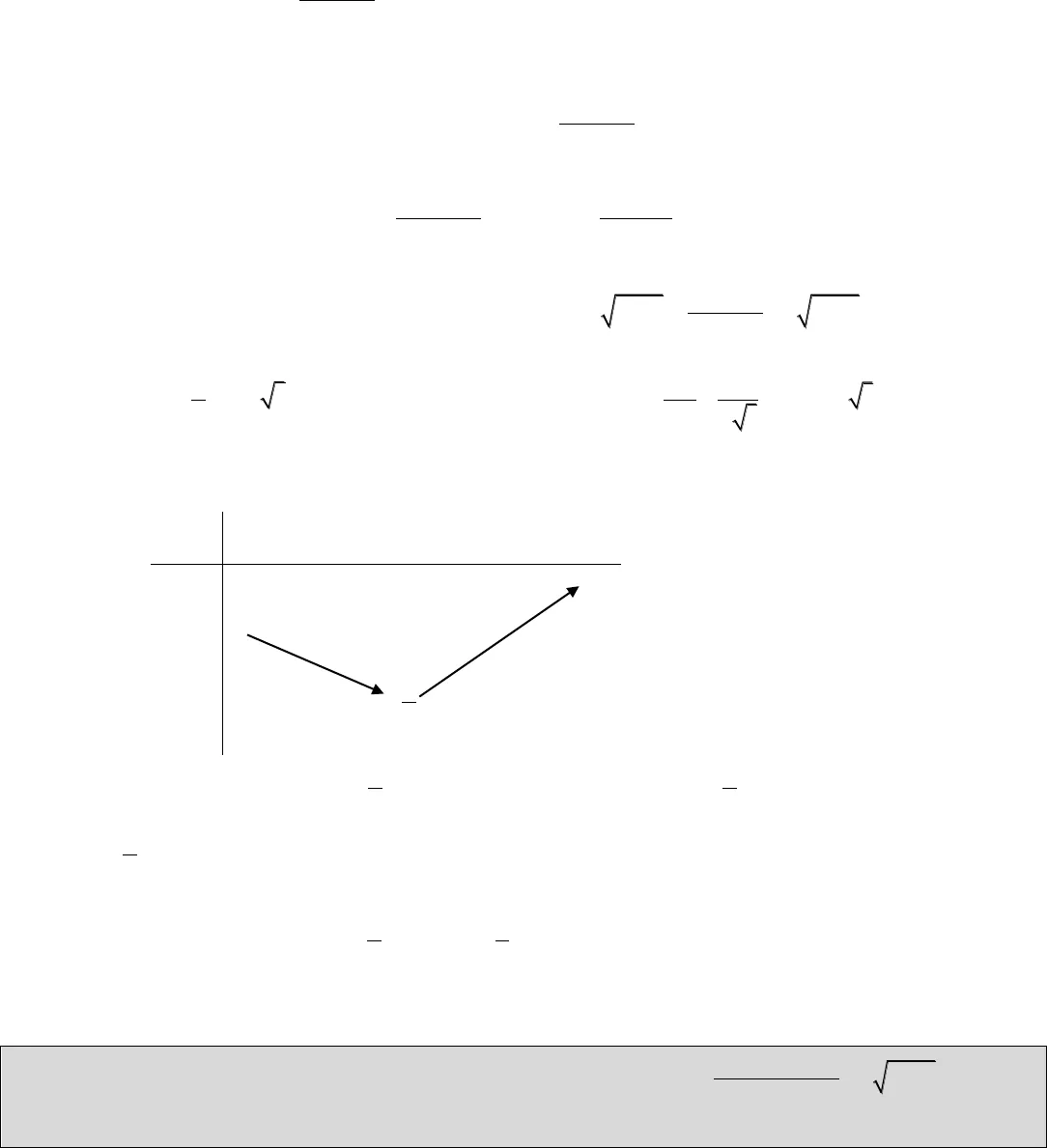 Biến đổi biểu thức: x y x y xy x y3333 , do đó nếu muốn sử dụng đánh giáx y x y33 , ta sẽ cần xy x y . Đánh giá cần tìm: xyxy24.Bài giảiTa có: x y x y xy x y3333 . Ta có đánh giá: xyxy24. Do đó: x y x yx y x y xy x y x y x y33333 3 3 33344 Đẳng thức xảy ra khi và chỉ khi: xy. Vậy: xyP x y x y x y3332 3 32 .Xét hàm số f t t t t313 , 02 . Ta có: P f x y. Vì: tf t t t tt2233′ 0 1 122 .Do đó ta có bảng biến thiên: t0 1 ft052Từ bảng biến thiên, ta thấy ft52 t, 0; . Vậy P f x y52 . Đẳng thức xảy ra khi và chỉkhixy12.Kết luận: Giá trị nhỏ nhất của Plà52tại xy12.Bài 2: Cho các số thực ,xydương. Tìm giá trị nhỏ nhất của biểu thức: P x yxy x y22188 .Phân tích Biến cần đưa về: xy. Chiều đánh giá cần có: P . Chiều cần đánh giá cần tìm: xy x y f x y22 .
Biến đổi biểu thức: x y x y xy x y3333 , do đó nếu muốn sử dụng đánh giáx y x y33 , ta sẽ cần xy x y . Đánh giá cần tìm: xyxy24.Bài giảiTa có: x y x y xy x y3333 . Ta có đánh giá: xyxy24. Do đó: x y x yx y x y xy x y x y x y33333 3 3 33344 Đẳng thức xảy ra khi và chỉ khi: xy. Vậy: xyP x y x y x y3332 3 32 .Xét hàm số f t t t t313 , 02 . Ta có: P f x y. Vì: tf t t t tt2233′ 0 1 122 .Do đó ta có bảng biến thiên: t0 1 ft052Từ bảng biến thiên, ta thấy ft52 t, 0; . Vậy P f x y52 . Đẳng thức xảy ra khi và chỉkhixy12.Kết luận: Giá trị nhỏ nhất của Plà52tại xy12.Bài 2: Cho các số thực ,xydương. Tìm giá trị nhỏ nhất của biểu thức: P x yxy x y22188 .Phân tích Biến cần đưa về: xy. Chiều đánh giá cần có: P . Chiều cần đánh giá cần tìm: xy x y f x y22 .
