Download.vn Học tập Lớp 9 Toán 9
Bạn đang đọc: 270 bài toán giải và biện luận phương trình bậc hai một ẩn
270 bài toán giải và biện luận phương trình bậc hai một ẩn Tài liệu ôn thi vào lớp 10 môn Toán
Giới thiệu Tải về Bình luận
- 5
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Với mong muốn đem đến cho các bạn học sinh lớp 9 có thêm nhiều tài liệu ôn tập môn Toán và thi vào lớp 10, Download.vn xin giới thiệu tài liệu 270 bài toán giải và biện luận phương trình bậc hai một ẩn.
Tài liệu gồm 101 trang tuyển tập 270 bài toán giải và biện luận phương trình bậc hai một ẩn nhằm phục vụ kỳ thi tuyển sinh lớp 10 THPT, lớp 10 hệ THPT chuyên. Nội dung chính gồm:
- Giải phương trình bậc hai bằng hằng đẳng thức
- Giải phương trình bậc hai bằng công thức nghiệm
- Giải phương trình bậc hai bằng công thức nghiệm thu gọn
- Giải và biện luận hệ phương trình bậc hai chứa tham số
- Câu hỏi phụ bài toán giải và biện luận
- Định lý Vi-et thuận – định lý Vi-et đảo
- Bài toán nhiều cách giải
270 bài toán giải và biện luận phương trình bậc hai một ẩn
 BÀI TẬP PHƯƠNG TRÌNH BẬC HAI (QUYỂN 1)_______________________________________________________________________________________________________________________________________________________________—————————————-————————————————————————————————-—————————————————-————————————————–CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN ĐỐNG ĐA; QUÂN ĐOÀN BỘ BINH3CCHHUUYYÊÊNNĐĐỀỀPPHHƯƯƠƠNNGGTTRRÌÌNNHH––BBẤẤTTPPHHƯƯƠƠNNGGTTRRÌÌNNHHTTRRUUNNGGHHỌỌCCCCƠƠSSỞỞBÀI TẬP PHƯƠNG TRÌNH BẬC HAI (QUYỂN 1)TTRRUUNNGGĐĐOOÀÀNNĐĐỐỐNNGGĐĐAA––QQUUÂÂNNĐĐOOÀÀNNBBỘỘBBIINNHH————-————————————————–———————–———————————————–——Trong khuôn khổ Toán học sơ cấp nói chung và Đại số phổ thông nói riêng, phương trình bậc nhất – phươngtrình bậc hai là dạng toán cơ bản nhưng có phạm vi trải rộng, phong phú, liên hệ chặt chẽ với nhiều bộ phận kháccủa toán học sơ cấp cũng như toán học hiện đại.Tại Việt Nam, hệ phương trình, nội dung phương trình – bất phương trình được song hành cùng hệ phươngtrình – hệ bất phương trình – hệ hỗn tạp là một bộ phận hữu cơ, quan trọng, được phổ biến giảng dạy chính thứctrong chương trình sách giáo khoa Toán các lớp 9, 10, 11, 12 song song với các khối lượng kiến thức liên quan. Nóiriêng về các phương pháp giải, biện luận phương trình bậc hai, nó được đề cập và luyện tập một cách đều đặn, bàibản và hệ thống sẽ rất hữu ích, không chỉ trong bộ môn Toán mà còn phục vụ đắc lực cho các môn khoa học tựnhiên khác như hóa học, vật lý, sinh học,….Đối với chương trình Đại số lớp 9 THCS hiện hành, phương trình bậchai là một nội dung cơ bản – quan trọng, xuất hiện bắt buộc trong Đề thi kiểm tra chất lượng học kỳ, Đề thi tuyểnsinh lớp 10 THPT hệ đại trà và hệ THPT Chuyên. Phương trình bậc hai khó có thể tạo ra bài toán rất khó, nhưng tạobài toán khó thì khá đơn giản, vì vậy đây luôn là kiến thức thường thấy trong các kỳ thi kiểm tra kiến thức thườngniên, kỳ thi chọn học sinh giỏi toán các cấp trên toàn quốc, kỳ thi tuyển sinh lớp 10 hệ THPT và trong kỳ thi tuyểnsinh đại học – cao đẳng hàng năm, một kỳ thi đầy cam go, kịch tính và bất ngờ, nó lại là một câu rất được quan tâmcủa các bạn học sinh, phụ huynh, các thầy cô, giới chuyên môn và đông đảo bạn đọc yêu Toán.Phương trình bậc hai dạng chính tắc 20, 0ax bx c a là một nội dung bắt buộc, thuộc phạm vi chươngtrình Đại số Học kỳ II Toán 9. Chúng ta thường bắt gặp phương trình gốc chứa tham số (m,n,k,a,…), kèm theo đólà nhiều câu hỏi phụ, với nội dung hết sức đa dạng, phong phú, gắn kết nhiều kiến thức, tác giả xin giới thiệu một sốtình huống đã từng gặp, từng học, từng biết như sau1. Trường hợp0a, phương trình bậc hai trở thành phương trình bậc nhất. 00 0 0, 00b ca bx c b ccx bb 2. Giải và biện luận phương trình bậc hai theo biệt thức24bac và công thức nghiệm.120:2bxxa , nghiệm kép (tức là hai nghiệm giống nhau, chập một).120: ; ;22bbx x x xaa , hai nghiệm phân biệt (khác nhau).0: Phương trình vô nghiệm.Như vậy, phương trình có nghiệm nghĩa là0.3. Tìm tham số để phương trình vô nghiệm; có nghiệm; có nghiệm kép; có hai nghiệm phân biệt.4. Tìm tham số để phương trình có một nghiệm bằng giá trịnào đó.Thayxvào phương trình ta có20ab c , từ đó tìm được tham số.5. Tìm tham số để phương trình không nhận nghiệm bằng giá trị nào đó.Phương trình không nhậnxlàm nghiệm khi20ab c .6. Tìm tham số để phương trình có hai nghiệm trái dấu. Khi đó nghiệm âm hay nghiệm dương có giá trị tuyệtđối lớn hơn (tùy thuộc đặc thù từng bài toán).
BÀI TẬP PHƯƠNG TRÌNH BẬC HAI (QUYỂN 1)_______________________________________________________________________________________________________________________________________________________________—————————————-————————————————————————————————-—————————————————-————————————————–CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN ĐỐNG ĐA; QUÂN ĐOÀN BỘ BINH3CCHHUUYYÊÊNNĐĐỀỀPPHHƯƯƠƠNNGGTTRRÌÌNNHH––BBẤẤTTPPHHƯƯƠƠNNGGTTRRÌÌNNHHTTRRUUNNGGHHỌỌCCCCƠƠSSỞỞBÀI TẬP PHƯƠNG TRÌNH BẬC HAI (QUYỂN 1)TTRRUUNNGGĐĐOOÀÀNNĐĐỐỐNNGGĐĐAA––QQUUÂÂNNĐĐOOÀÀNNBBỘỘBBIINNHH————-————————————————–———————–———————————————–——Trong khuôn khổ Toán học sơ cấp nói chung và Đại số phổ thông nói riêng, phương trình bậc nhất – phươngtrình bậc hai là dạng toán cơ bản nhưng có phạm vi trải rộng, phong phú, liên hệ chặt chẽ với nhiều bộ phận kháccủa toán học sơ cấp cũng như toán học hiện đại.Tại Việt Nam, hệ phương trình, nội dung phương trình – bất phương trình được song hành cùng hệ phươngtrình – hệ bất phương trình – hệ hỗn tạp là một bộ phận hữu cơ, quan trọng, được phổ biến giảng dạy chính thứctrong chương trình sách giáo khoa Toán các lớp 9, 10, 11, 12 song song với các khối lượng kiến thức liên quan. Nóiriêng về các phương pháp giải, biện luận phương trình bậc hai, nó được đề cập và luyện tập một cách đều đặn, bàibản và hệ thống sẽ rất hữu ích, không chỉ trong bộ môn Toán mà còn phục vụ đắc lực cho các môn khoa học tựnhiên khác như hóa học, vật lý, sinh học,….Đối với chương trình Đại số lớp 9 THCS hiện hành, phương trình bậchai là một nội dung cơ bản – quan trọng, xuất hiện bắt buộc trong Đề thi kiểm tra chất lượng học kỳ, Đề thi tuyểnsinh lớp 10 THPT hệ đại trà và hệ THPT Chuyên. Phương trình bậc hai khó có thể tạo ra bài toán rất khó, nhưng tạobài toán khó thì khá đơn giản, vì vậy đây luôn là kiến thức thường thấy trong các kỳ thi kiểm tra kiến thức thườngniên, kỳ thi chọn học sinh giỏi toán các cấp trên toàn quốc, kỳ thi tuyển sinh lớp 10 hệ THPT và trong kỳ thi tuyểnsinh đại học – cao đẳng hàng năm, một kỳ thi đầy cam go, kịch tính và bất ngờ, nó lại là một câu rất được quan tâmcủa các bạn học sinh, phụ huynh, các thầy cô, giới chuyên môn và đông đảo bạn đọc yêu Toán.Phương trình bậc hai dạng chính tắc 20, 0ax bx c a là một nội dung bắt buộc, thuộc phạm vi chươngtrình Đại số Học kỳ II Toán 9. Chúng ta thường bắt gặp phương trình gốc chứa tham số (m,n,k,a,…), kèm theo đólà nhiều câu hỏi phụ, với nội dung hết sức đa dạng, phong phú, gắn kết nhiều kiến thức, tác giả xin giới thiệu một sốtình huống đã từng gặp, từng học, từng biết như sau1. Trường hợp0a, phương trình bậc hai trở thành phương trình bậc nhất. 00 0 0, 00b ca bx c b ccx bb 2. Giải và biện luận phương trình bậc hai theo biệt thức24bac và công thức nghiệm.120:2bxxa , nghiệm kép (tức là hai nghiệm giống nhau, chập một).120: ; ;22bbx x x xaa , hai nghiệm phân biệt (khác nhau).0: Phương trình vô nghiệm.Như vậy, phương trình có nghiệm nghĩa là0.3. Tìm tham số để phương trình vô nghiệm; có nghiệm; có nghiệm kép; có hai nghiệm phân biệt.4. Tìm tham số để phương trình có một nghiệm bằng giá trịnào đó.Thayxvào phương trình ta có20ab c , từ đó tìm được tham số.5. Tìm tham số để phương trình không nhận nghiệm bằng giá trị nào đó.Phương trình không nhậnxlàm nghiệm khi20ab c .6. Tìm tham số để phương trình có hai nghiệm trái dấu. Khi đó nghiệm âm hay nghiệm dương có giá trị tuyệtđối lớn hơn (tùy thuộc đặc thù từng bài toán).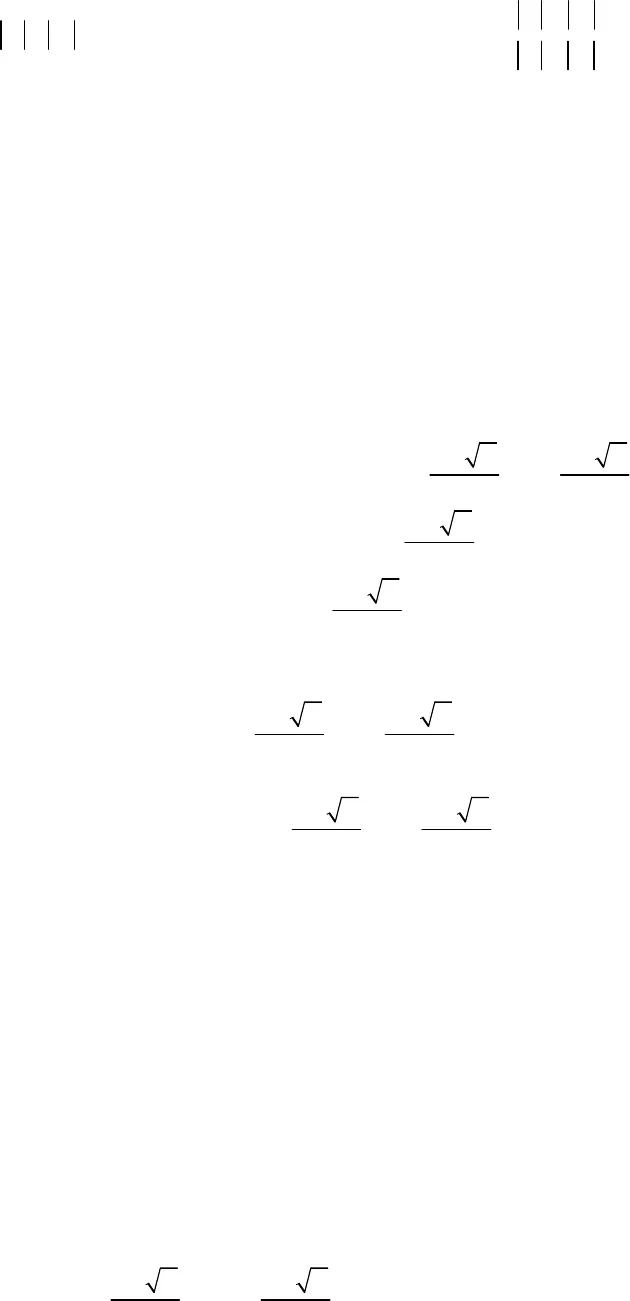 BÀI TẬP PHƯƠNG TRÌNH BẬC HAI (QUYỂN 1)_______________________________________________________________________________________________________________________________________________________________—————————————-————————————————————————————————-—————————————————-————————————————–CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN ĐỐNG ĐA; QUÂN ĐOÀN BỘ BINH4Hai nghiệm trái dấu khi0ac. Rõ ràng nếu tổng hai nghiệm dương thì nghiệm dương có giá trị tuyệt đốilớn hơn, tổng hai nghiệm âm thì nghiệm âm có giá trị tuyệt đối lớn hơn. Để dễ hình dung, các bạn có thể giảsử 12 1 2 1 2 1 20xx x x x x x x , dẫn đến12 1 212 1 200x x x xx x x x 7. Tìm tham số để phương trình có hai nghiệm cùng dấu, khi đó hai nghiệm mang dấu gì (tùy thuộc đặc thùtừng bài toán).Hai nghiệm cùng dấu khi0ac. Nếu tổng hai nghiệm dương thì hai nghiệm cùng dương, tổng hai nghiệmâm thì hai nghiệm cùng âm.8. Tìm tham số để phương trình có hai nghiệm cùng dương, hai nghiệm cùng âm.9. Tìm tham số để phương trình có đúng một nghiệm âm, có đúng một nghiệm dương (lưu ý đây chưa chắcchắn là trường hợp hai nghiệm trái dấu, trường hợp này cần xét khả năng đặc biệt nghiệm bằng 0).Phương trình có đúng một nghiệm âm bao gồm các trường hợp một nghiệm bằng 0 – một nghiệm âm; hainghiệm trái dấu; nghiệm kép âm.Phương trình có đúng một nghiệm dương bao gồm các trường hợp một nghiệm bằng 0 – một nghiệmdương; hai nghiệm trái dấu; nghiệm kép dương.10. Tìm tham số để phương trình có (tồn tại) nghiệm lớn hơn hoặc nhỏ hơn một hằng số nào đó.Phương trình có (tồn tại) nghiệm lớn hơn hằng số nào đó khi nghiệm lớn nhất lớn hơn hằng số đó, thôngthường nếu hệ số a là hằng số các bạn lập tức khẳng định22bbx xaa .Khi đó, phương trình tồn tại một nghiệm lớn hơn2bxa .Phương trình tồn tại một nghiệm nhỏ hơn2bxa .11. Tìm tham số để phương trình có cả hai nghiệm lớn hơn hoặc nhỏ hơn một hằng số nào đó.Theo mục 10, nếu nghiệm lớn hơn mà nhỏ hơn hằng số thì cả hai nghiệm sẽ nhỏ hơn hằng số, tức là22bbx xaa Nghiệm nhỏ hơn mà lớn hơn hằng số thì cả hai nghiệm sẽ lớn hơn hằng số22bbx xaa .Hiểu nôm na: Anh đứng đầu thua thì tất cả những anh khác phía sau sẽ thua. Anh đứng cuối thắng thì tất cảnhững anh đứng phía trên đều thắng.Ngoài ra các bạn có thể sử dụng hệ thức Viete với lập luận 1211 2220xxxx xx hoặc 1211 2220xxxx xx Thêm nữa, có thể đặt đặt ẩn phụx t x t . Khi đó dẫn đến bài toán phụ tìm tham số để phươngtrình bậc hai 20at b t c có hai nghiệm cùng dấu.12. Tìm tham số để phương trình có hai nghiệm nằm về hai phía của một hằng số12x x . Khi đó rõ ràngcác bạn thấy 1122000xxxx .13. Tìm tham số để phương trình có nghiệm nằm trong đoạn [a;b], khoảng (a;b) nào đó (đối với một hoặc cả hainghiệm).Các bạn làm thủ công;22bbab a baa . Nếu biệt thức chính phương hằng số hoặc chínhphương biểu thức thì điều này khá đơn giản do tính được hai nghiệm gọn gàng.
BÀI TẬP PHƯƠNG TRÌNH BẬC HAI (QUYỂN 1)_______________________________________________________________________________________________________________________________________________________________—————————————-————————————————————————————————-—————————————————-————————————————–CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN ĐỐNG ĐA; QUÂN ĐOÀN BỘ BINH4Hai nghiệm trái dấu khi0ac. Rõ ràng nếu tổng hai nghiệm dương thì nghiệm dương có giá trị tuyệt đốilớn hơn, tổng hai nghiệm âm thì nghiệm âm có giá trị tuyệt đối lớn hơn. Để dễ hình dung, các bạn có thể giảsử 12 1 2 1 2 1 20xx x x x x x x , dẫn đến12 1 212 1 200x x x xx x x x 7. Tìm tham số để phương trình có hai nghiệm cùng dấu, khi đó hai nghiệm mang dấu gì (tùy thuộc đặc thùtừng bài toán).Hai nghiệm cùng dấu khi0ac. Nếu tổng hai nghiệm dương thì hai nghiệm cùng dương, tổng hai nghiệmâm thì hai nghiệm cùng âm.8. Tìm tham số để phương trình có hai nghiệm cùng dương, hai nghiệm cùng âm.9. Tìm tham số để phương trình có đúng một nghiệm âm, có đúng một nghiệm dương (lưu ý đây chưa chắcchắn là trường hợp hai nghiệm trái dấu, trường hợp này cần xét khả năng đặc biệt nghiệm bằng 0).Phương trình có đúng một nghiệm âm bao gồm các trường hợp một nghiệm bằng 0 – một nghiệm âm; hainghiệm trái dấu; nghiệm kép âm.Phương trình có đúng một nghiệm dương bao gồm các trường hợp một nghiệm bằng 0 – một nghiệmdương; hai nghiệm trái dấu; nghiệm kép dương.10. Tìm tham số để phương trình có (tồn tại) nghiệm lớn hơn hoặc nhỏ hơn một hằng số nào đó.Phương trình có (tồn tại) nghiệm lớn hơn hằng số nào đó khi nghiệm lớn nhất lớn hơn hằng số đó, thôngthường nếu hệ số a là hằng số các bạn lập tức khẳng định22bbx xaa .Khi đó, phương trình tồn tại một nghiệm lớn hơn2bxa .Phương trình tồn tại một nghiệm nhỏ hơn2bxa .11. Tìm tham số để phương trình có cả hai nghiệm lớn hơn hoặc nhỏ hơn một hằng số nào đó.Theo mục 10, nếu nghiệm lớn hơn mà nhỏ hơn hằng số thì cả hai nghiệm sẽ nhỏ hơn hằng số, tức là22bbx xaa Nghiệm nhỏ hơn mà lớn hơn hằng số thì cả hai nghiệm sẽ lớn hơn hằng số22bbx xaa .Hiểu nôm na: Anh đứng đầu thua thì tất cả những anh khác phía sau sẽ thua. Anh đứng cuối thắng thì tất cảnhững anh đứng phía trên đều thắng.Ngoài ra các bạn có thể sử dụng hệ thức Viete với lập luận 1211 2220xxxx xx hoặc 1211 2220xxxx xx Thêm nữa, có thể đặt đặt ẩn phụx t x t . Khi đó dẫn đến bài toán phụ tìm tham số để phươngtrình bậc hai 20at b t c có hai nghiệm cùng dấu.12. Tìm tham số để phương trình có hai nghiệm nằm về hai phía của một hằng số12x x . Khi đó rõ ràngcác bạn thấy 1122000xxxx .13. Tìm tham số để phương trình có nghiệm nằm trong đoạn [a;b], khoảng (a;b) nào đó (đối với một hoặc cả hainghiệm).Các bạn làm thủ công;22bbab a baa . Nếu biệt thức chính phương hằng số hoặc chínhphương biểu thức thì điều này khá đơn giản do tính được hai nghiệm gọn gàng.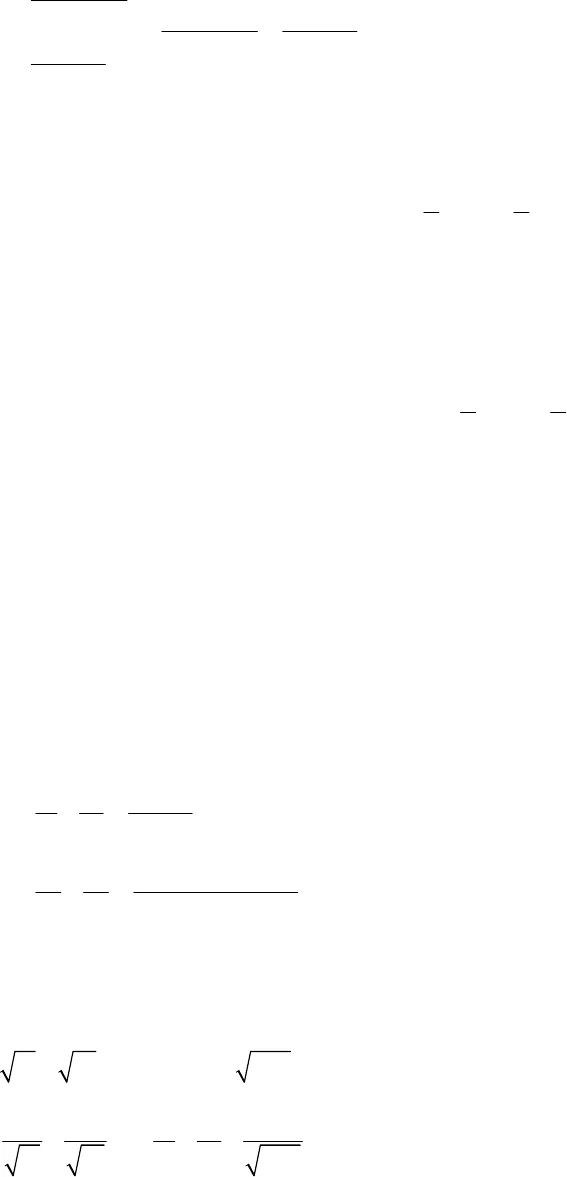 BÀI TẬP PHƯƠNG TRÌNH BẬC HAI (QUYỂN 1)_______________________________________________________________________________________________________________________________________________________________—————————————-————————————————————————————————-—————————————————-————————————————–CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN ĐỐNG ĐA; QUÂN ĐOÀN BỘ BINH514. Tìm hệ thức liên hệ giữa hai nghiệm không phụ thuộc tham số, các bạn có thể cô lập tham số (biểu diễntham số theo hai cách) hoặc cộng đại số giữa tổng và tích hai nghiệm để triệt tiêu tham số.Thí dụ121 21 2 1 21 21 234 33 7475 74 55x xmx x mx x x xx xx x mm .15. Tìm tham số để phương trình có hai nghiệm thỏa mãn một hệ thức nào đó (hệ thức bậc nhất mang tính đốixứng đối với hai nghiệm), sử dụng định lý Viete thuần túy.Các bạn không nên vội vàng, trước hết tìm điều kiện để phương trình là phương trình bậc hai và có nghiệm0, đây chính là điều kiện tiên quyết áp dụng hệ thức Viete12 1 2;bcxx x xaa .Tiếp sau chú ý kết hợp giải hệ phương trình theo tham số (gồm tổng và hệ thức đề bài đưa ra). Tính tích hainghiệm và thu được kết quả.16. Tìm tham số để phương trình có hai nghiệm thỏa mãn một hệ thức nào đó (hệ thức bậc hai, bậc cao mangtính đối xứng với hai nghiệm), sử dụng định lý Viete thuần túy.Các bạn không nên vội vàng, trước hết tìm điều kiện để phương trình là phương trình bậc hai và có nghiệm0, đây chính là điều kiện tiên quyết áp dụng hệ thức Viete12 1 2;b cxx x xaa . Sau đó có cơ sở,muốn làm gì thì làm (nói vui), lưu ý các hệ thức đối xứng 2221 2 1 2 1 22 21 2 1 2 1 22 21 2 2 1 1 2 1 233 3 2 212 1 2 1 1 2 2 1 2 1 2 1 2244 2 2 2 21 2 1 2 1 22432x x x x x xx x x x x xx x x x x x x xx x x x x x x x x x x x x xx x x x x x 17. Tìm tham số để phương trình có hai nghiệm thỏa mãn một thức nào đó (hệ thức chứa phân thức, mang tínhđối xứng với hai nghiệm), sử dụng định lý Viete thuần túy.Lưu ý tìm điều kiện mẫu thức khác 0 khi biến đổi 121 21 2 1 221 2 1 21 22 2 2 21 2 1 21 1021 10x xx xx x x xx x x xx xx x x x 18. Tìm tham số để phương trình có hai nghiệm thỏa mãn một hệ thức nào đó (hệ thức chứa căn thức, mang tínhđối xứng với hai nghiệm), sử dụng định lý Viete thuần túy.Đối với hệ thức chứa căn cần tìm tham số để một trong hai nghiệm (hoặc hai nghiệm cùng không âm) trướctiên, đó là điều kiện để căn thức có nghĩa. 212 1 2 1 2 1 221 21 21 2 1 22 0; 01 1 1 1 10; 0x x x x x x x xx xx xx x x x 19. Tìm tham số để phương trình có hai nghiệm thỏa mãn một hệ thức nào đó (hệ thức chứa giá trị tuyệt đối,mang tính đối xứng với hai nghiệm), sử dụng định lý Viete thuần túy.Với biểu thức chứa giá trị tuyệt đối cũng cần hết sức chú ý, đại ý như 2255;5AA , trong khi đó Axuất phát điểm là một biểu thức trong dấu giá trị tuyệt đối, thế thì5A.
BÀI TẬP PHƯƠNG TRÌNH BẬC HAI (QUYỂN 1)_______________________________________________________________________________________________________________________________________________________________—————————————-————————————————————————————————-—————————————————-————————————————–CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN ĐỐNG ĐA; QUÂN ĐOÀN BỘ BINH514. Tìm hệ thức liên hệ giữa hai nghiệm không phụ thuộc tham số, các bạn có thể cô lập tham số (biểu diễntham số theo hai cách) hoặc cộng đại số giữa tổng và tích hai nghiệm để triệt tiêu tham số.Thí dụ121 21 2 1 21 21 234 33 7475 74 55x xmx x mx x x xx xx x mm .15. Tìm tham số để phương trình có hai nghiệm thỏa mãn một hệ thức nào đó (hệ thức bậc nhất mang tính đốixứng đối với hai nghiệm), sử dụng định lý Viete thuần túy.Các bạn không nên vội vàng, trước hết tìm điều kiện để phương trình là phương trình bậc hai và có nghiệm0, đây chính là điều kiện tiên quyết áp dụng hệ thức Viete12 1 2;bcxx x xaa .Tiếp sau chú ý kết hợp giải hệ phương trình theo tham số (gồm tổng và hệ thức đề bài đưa ra). Tính tích hainghiệm và thu được kết quả.16. Tìm tham số để phương trình có hai nghiệm thỏa mãn một hệ thức nào đó (hệ thức bậc hai, bậc cao mangtính đối xứng với hai nghiệm), sử dụng định lý Viete thuần túy.Các bạn không nên vội vàng, trước hết tìm điều kiện để phương trình là phương trình bậc hai và có nghiệm0, đây chính là điều kiện tiên quyết áp dụng hệ thức Viete12 1 2;b cxx x xaa . Sau đó có cơ sở,muốn làm gì thì làm (nói vui), lưu ý các hệ thức đối xứng 2221 2 1 2 1 22 21 2 1 2 1 22 21 2 2 1 1 2 1 233 3 2 212 1 2 1 1 2 2 1 2 1 2 1 2244 2 2 2 21 2 1 2 1 22432x x x x x xx x x x x xx x x x x x x xx x x x x x x x x x x x x xx x x x x x 17. Tìm tham số để phương trình có hai nghiệm thỏa mãn một thức nào đó (hệ thức chứa phân thức, mang tínhđối xứng với hai nghiệm), sử dụng định lý Viete thuần túy.Lưu ý tìm điều kiện mẫu thức khác 0 khi biến đổi 121 21 2 1 221 2 1 21 22 2 2 21 2 1 21 1021 10x xx xx x x xx x x xx xx x x x 18. Tìm tham số để phương trình có hai nghiệm thỏa mãn một hệ thức nào đó (hệ thức chứa căn thức, mang tínhđối xứng với hai nghiệm), sử dụng định lý Viete thuần túy.Đối với hệ thức chứa căn cần tìm tham số để một trong hai nghiệm (hoặc hai nghiệm cùng không âm) trướctiên, đó là điều kiện để căn thức có nghĩa. 212 1 2 1 2 1 221 21 21 2 1 22 0; 01 1 1 1 10; 0x x x x x x x xx xx xx x x x 19. Tìm tham số để phương trình có hai nghiệm thỏa mãn một hệ thức nào đó (hệ thức chứa giá trị tuyệt đối,mang tính đối xứng với hai nghiệm), sử dụng định lý Viete thuần túy.Với biểu thức chứa giá trị tuyệt đối cũng cần hết sức chú ý, đại ý như 2255;5AA , trong khi đó Axuất phát điểm là một biểu thức trong dấu giá trị tuyệt đối, thế thì5A.
