Download.vn Học tập Lớp 10
Bạn đang đọc: Bài tập cơ học chất điểm
Bài tập cơ học chất điểm Tài liệu ôn thi học sinh giỏi môn Vật lý lớp 10
Giới thiệu Tải về Bình luận
- 1
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Với mong muốn đem đến cho các bạn học sinh lớp 10 có thêm nhiều tài liệu ôn thi học sinh giỏi môn Vật lý, Download.vn xin giới thiệu đến các bạn tài liệu Bài tập cơ học chất điểm được chúng tôi tổng hợp và đăng tải ngay sau đây.
Bài tập cơ học chất điểm ôn thi học sinh giỏi là tài liệu tham khảo hay, giúp cho các bạn học sinh tự luyện tập, ôn lại kiến thức nhằm bồi dưỡng học sinh giỏi môn vật lý lớp 10. Tài liệu này bao gồm các bài tập và đáp án về phần cơ học chất điểm. Mời các bạn cùng tham khảo.
Bài tập cơ học chất điểm ôn thi học sinh giỏi
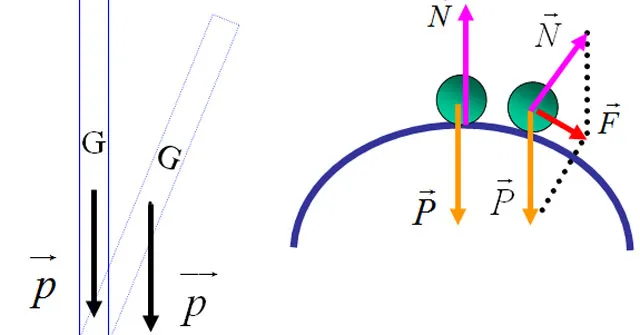
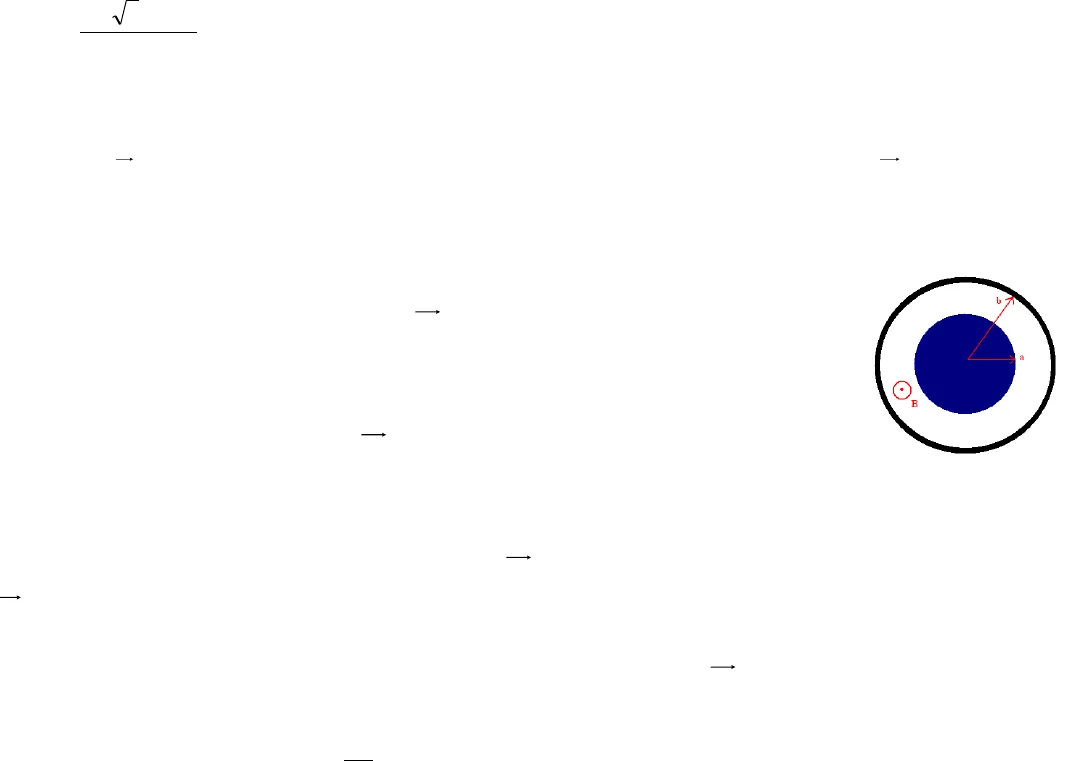BÀI TẬP CƠ HỌC CHẤT ĐIỂM Bài 1. Một mặt đĩa tròn bán kính R quay quanh trục thẳng đứng với vận tốc góc. Từ tâm đĩa một con bọ bò dọc theo bán kính với tốc độ không đổi v0so với đĩa. Xét trong hệ qui chiếu gắn với đất hãy xác định:a. Phương trình chuyển động và phương trình quỹ đạo của con bọ. b. Biểu thức vận tốc và gia tốc của con bọ. c.Bán kính cong của quỹ đạo theo thời gian. d.Quãng đường con bọ đi được so với đất. Bài 2. (Bốn con rùa). Trên mặt phẳng, tại bốn đỉnh của một hình vuông cạnh a, có bốn con rùa nhỏ. Theo hiệu lệnh chúng bắt đầu chuyển động với vận tốc có độ lớn vokhông đổi. Biết rằng tại thời điểm bất kỳ, mỗi con ra đều chuyển động hướng đúng về phía con ra bên cạnh theo chiều kim đồng hồ. Coi mỗi con rùa là một chất điểm. a. viết phương trình chuyển động của mỗi con rùa. Từ đó suy ra phương trình quỹ đạo của chúng.b. Tìm gia tốc của rùa phụ thuộc vào thời gian.c. Tìm bán kính cong quay đạo của mỗi con rùa theo thời gian. Coi mỗi con rùa là một chất điểmBài 3. Trên mặt phẳng, tại ba đỉnh của một tam giác đều, cạnh L, có ba con rùa nhỏ. Theo hiệu lệnh chúng bắt đầu chuyển động với vận tốc có độ lớn vokhông đổi. Biết rằng tại thời điểm bất kỳ, mỗi con ra đều chuyểnđộng hướng đúng về phía con ra bên cạnh theo chiều kim đồng hồ. Tìm gia tốc của rùa phụ thuộc vào thời gian. ĐS: a = )5,1(2.32tvLvooBài 4. Trên một mặt phẳng ngang nhẵn có quả cầu nhỏ được coi là chất điểm, khối lượng m, buột vào đầu một sợi dây mãnh không dãn khối lượng không đáng kể. Một đầu sợi dây luồn qua một lỗ nhỏ xuyên qua mặt phẳngngang. Ban đầu, dây thẳng và đoạn dây trên mặt phẳng ngang có chiều dàil, người ta cung cấp cho quả cầu vận tốc đầu1vhướng vuông góc với sợi dây, đồng thời đầu còn lại sợi dây kéo với vận tốc 0vkhông đổi. Hãy tìm lực căng dây, tốc độ theo r và bán kính cong quỹ đạo chuyển động của quả cầu. Bài 5. Khoảng không gian giữa một cặp vật dẫn hình trụ đồng trục đã được rút chân không. Bán kính hình trị trụ trong là a, bán kính trong của hình trụ ngoài là b (hình vẽ). Hình trụ ngoài gọi là anot và có thể đặt ở điện thế dương hơn so với hình trụ trong là U. Người ta thiết lập một từ trường không đổi, đồng nhất (đều)Bsong song với trục hình trụ và hướng từmặt hình vẽ lên phía trên. Bỏ qua các điện tích cảm ứng trên các vật dẫn.Trong bài này ta nghiên cứu động lực học của electron khối lượng nghỉ m, tích điện – e ; các electron này phát ra từ bề mặt của hình trụ trong.a) Thoạt đầu ta đặt điện thế V nhưng B= 0. Các electron được giải phóng từ mặt khối trụ trong với vận tốc không đáng kể. Hãy tính tốc độ của nó khi nó đập vào anot; cho kết quả trong 2 trường hợp: phi tương đối tính và tương đối tính.Trong các phần còn lại của bài toán chỉ xét trường hợp phi tương đối tính.b) Bây giờ cho U = 0 và cho tác dụng của từ trườngB. Một electron phát ra theo phương bán kính với vận tốc 0v. Khi từ trường lớn hơn một giá trị tới hạn BC, electron không tới được anot. Vẽ quỹ đạo của electron khi Bhơi lớn hơn BC.Từ đây về sau, ta cho tác dụng đồng thời của V và từ trường đồng nhất B.c) Từ trường sẽ gây ra cho electron một momen động lượng đối với trục hình trụ khác không. Hãy viết một phương trình cho ta tốc độ thay đổi dtdLcủa momen động lượng.Chứng tỏ phương trình đó nói lên đại lượng ( L – KeBr2) không thay đổi khi electron chuyển động, trong đó Klà một số xác định không có thứ nguyên, r là khoảng cách tính đến trục hình trụ. Xác định giá trị của K.
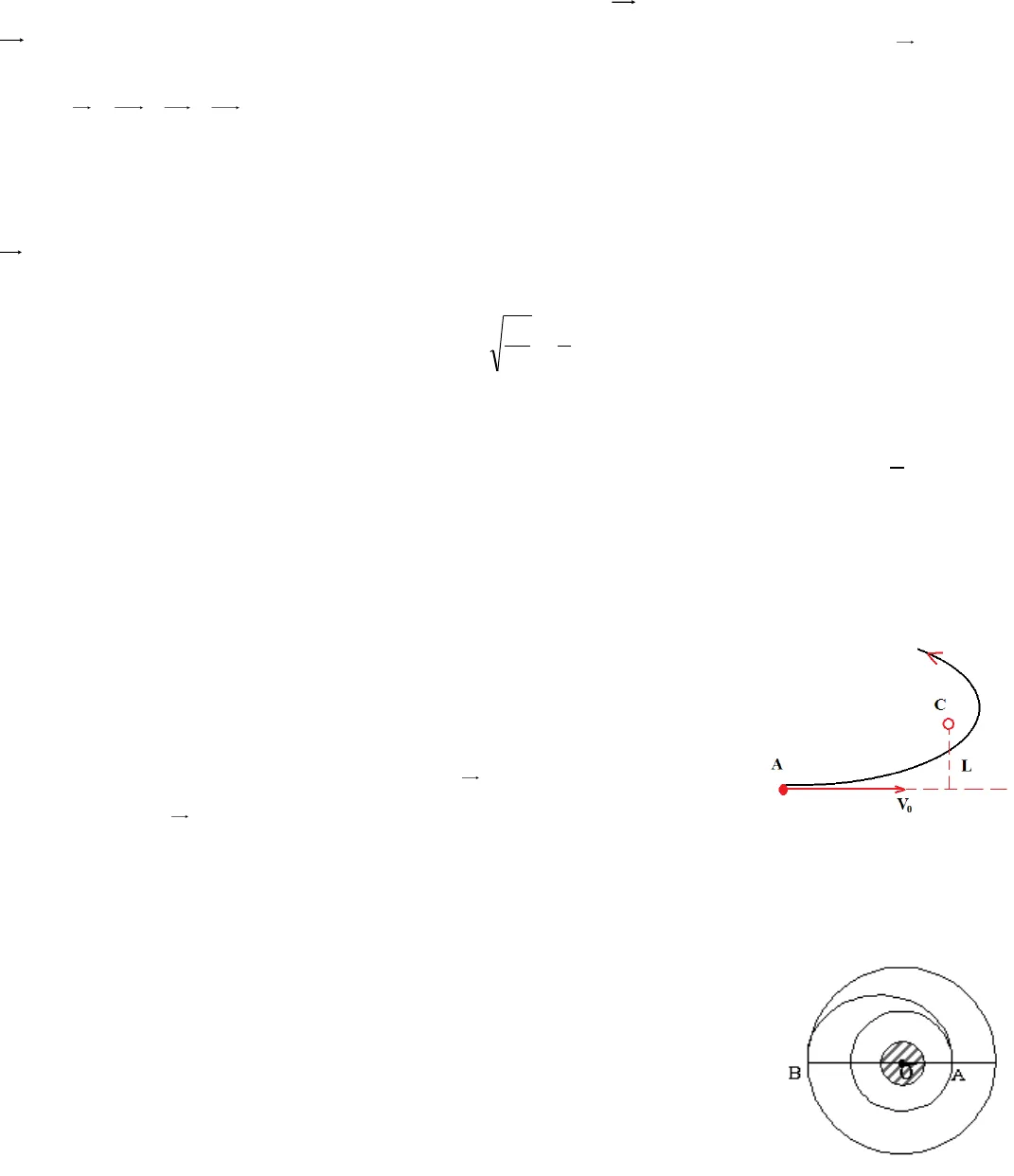d) Xét một electron phát ra hình trụ trong với tốc độ không đáng kể và không đến được anot, nhưng đạt được khoảng cách tối đa rmđối với trục hình trụ. Xác định tốc độ v tại điểm mà khoảng cách theo phương bán kính là lớn nhất theo rm.e) Chúng ta muốn dùng từ trường để điều khiển dòng electron đi tới anot. Với B lớn hơn từ trường tới hạn BCthì electron phát ra từ bề mặt khối trụ trong với vận tốc không đáng kể sẽ không đến được anot. Xác định BC?f) Nếu electron được phát ra bằng cách đốt nóng khối trụ trong, thì chúng có thể có tốc độ khác không ở bề mặt khối trụ trong. Thành phần tốc độ ban đầu thứ nhất song song với Blà vB, thành phần thứ hai vuông góc với Blà vr(theo phương bán kính) và thành phần thứ bav(theo phương vuông góc với bán kínhr). Hãy xác định từ trường tới hạn để elctron đạt tới anot trong bối cảnh ấy(Nghĩa là khi phát xạ nhiệt ra electron có vận tốc Brv v v v ) Bài 6. Một vật khối lượng 2m được coi là chất điểm đặt ở đỉnh của một đường trượt ( C) có dạng parabol với phương trình trong toạ độ oxy ( trong mặt phẳng thẳng đứng ) : y = a x2(m); a = 20 ( m-1), x tính bằng m . Một viên đạn khối lượng m bay theo phương ngang với vận tốc 0vđến va chạm mềm với chất điểm nói trên . Tìm điều kiện v0để vật luôn trượt trên đường ( C) nói trên . ( Bỏqua ma sát )ĐS: + Để vật vẫn trượt trên đường cong ( c ) thì 23a2g9v0(m/s)+ Nếu v > 3/2 ( m/s ) thì hệ chuyển động không thể tiếp xúc đường trượt .Bài 7. Để công kích mục tiêu người ta phóng tên lửa từ máy bay. Máy bay bay ngang ở độ cao H = 8km với vận tốc v0= 300m/s. Khối lượng tên lửa biến đổi theo quy luật tmtm exp)(0và giảm elần cho tới khi bay tới mục tiêu. Vận tốc khí phụt ra đối với tên lửa u = 1000m/s, thân tên lửa nằm ngang trong thời gian bay. Hỏi khoảng cách L từ mục tiêu tới vị trí máy bay tại thời điểm phóng bằngbao nhiêu? Bỏ qua lực cản của không khí.Bài 8. Một con tàu vũ trụ được phóng lên chuyển động quanh trái đất theo quỹ đạo Elíp có bán trục lớn a, bán trục nhỏ b. Biết trái đất có khối lượng M và nằm một trong hai tiêu điểm Elíp. a. Hãy xác định bán kính cong quỹ đạo tại cận điểm A và viễn điểm B. b. Xác định cơ năng của con tàu. c . Hãy xác định vận tốc tại cận điểm A và viễn điểm B. d. Xác định vận tốc của con tàu tại vị trí cách tâm trái đất một khoảng r. Bài 9. Một thiên thể A chuyển động tới Mặt Trời; khi còn ở cách xa Mặt Trời(thế năng khi đó bằng không), nó có vận tốc 0vvà tham số ngắm L là cánhtay đòn của vec tơ0vđối với tâm Mặt Trời (hình vẽ) . Tìm khoảng cách nhỏ nhất mà vật này có thể lại gần Mặt trời.Bài 10. Vệ tinh chuyển động tròn ở độ cao ho= Ro(Robán kính Trái Đất ). Người ta muốn chuyển nó lên quỹđạo tròn ở độ cao H = 3Robằng quỹ đạo nửa elip AB tiếp xúc với hai quỹ đạo tròn ở A và B, các điểm AOBthẳng hàng. Cần tăng hoặc giảm bao nhiêu vận tốc ở các điểm A và B ( tăng giảmrất nhanh). Biết vận tốc vũ trụ ở sát mặt đất là v1= 7.9km/s.Đáp số Vậy độ tăng vận tốc : ở A l 6,44 – 5,58 = 0,86 (km/s); ở B l 3,95 – 3,22 = 0,73 (km/s)Bài 11. Một vệ tinh nhân tạo của Mặt Trăng chuyển động theo một quỹ đạo tròn có bán kính lớn hơn bán kính Mặt Trăng lần. Khi chuyển động, vệ tinh chịu một sức cản yếu của bụi vũ trụ. Giả thử rằng lực cản phụ thuộc vào vận tốc của vệ tinh theo định luật 2Fv, trong đólà một hằng số; tìm thời gian chuyển động của 
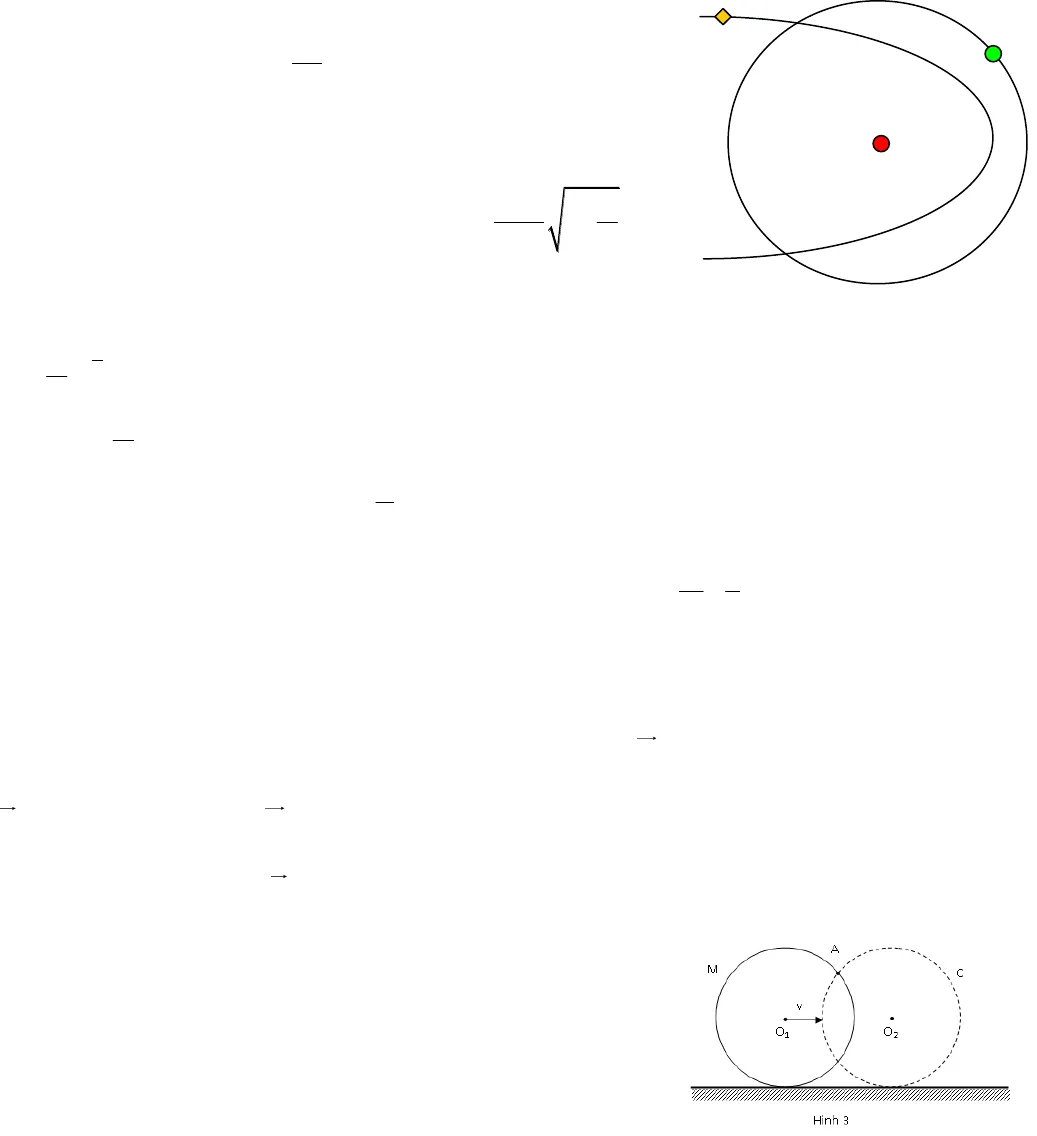CTSvệ tinh cho tới lúc nó rơi lên bề mặt Mặt Trăng.Bài 12. Hãy tìm thời gian cực đại mà sao chổi (C) có khối lượng m chuyển động theo quỹ đạo parabol xung quanh mặt trời (S) tồn tại bên trong vùng quỹ đạo tròn của trái đất (T). Cho rằng các quỹ đạo của trái đất và sao chổi nằm trong cùng một mặt phẳng (xem hình vẽ) ĐS:maxt 77ngày Bài 13. Hạt với khối lượng m chuyển động theo đường tròn bán kính R dưới tác dụng của lực xuyên tâm :a/r2erKFa. Hãy xác định điều kiện cho hằng số a để quỹ đạo tròn là ổn định b. Hãy tính tần số của dao động xuyên tâm bé theo các hướng xuyên tâm của quỹđạo tròn. ĐS: a. Để trạng thái là cân bằng cần có a > R; b.21lRmR aBài 14. Một dây cao su AB đàn hồi lý tưởng chiều dài L, đầu A gắn với tường, đầu B còn lại đặt một con kiến. Tại thời điểm t=0 kéo đầu B với vận tốc V ra xa tường. Cùng lúc ấy, con kiến đi về phía tường với vận tốc u so với dây. Con kiến đến được tường trong điều kiện nào? Thời gian bao lâu? Đáp số:( 1)VuLteV Biện luận: +Nếu uVrất lớn so với 1 thì t khá lớn + Nếu V/u rất bé so với 1 thìuLt Bài 15. Thế năng của một hạt trong một trường hấp dẫn nào đó có dạng 2abUrr, với a và b là các hằng sốdương, r là khoảng cách tính từ tâm của trường. Hãy tìm: a) giá trị r0tương ứng với vị trí cân bằng của hạt. Hãy giải thích vị trí này có phải là vị trí cân bằng bên không?b) giá trị cực đại của lực hấp dẫnc) hãy biểu diễn áng chừng đồ thị sự phụ thuộc U(r) và F(r) là hình chiếu của lực lên bán kính vectơ r.Bài 16. Một hạt tích điện q bay vào trong một môi trường có vận tốc đầu 0v. Hạt chịu lực cản của môi trường tỉlệ với vận tốc và đi được một đoạn a= 10cm thì dừng lại. Khi tạo ra trong môi trường một từ trường đều có cảmứng từ Bvuông góc vận tốc đầu 0vthì hạt đó chuyển động cong và dừng lại tại một điểm cách điểm xuất phát một đoạn b=6cm. Hỏi nếu độ lớn của cảm ứng từBgiảm một nửa thì nó dừng lại cách điểm ban đầu một đọan c bằng baonhiêu?( Bỏ qua tác dụng của trọng lực) ĐS: c= 8,32cm. Bài 17. Trên mặt phẳng thẳng đứng P có vẽ một vòng tròn C bán kính R tâm O2tiếp xúc với mặt phẳng ngang. Một chiếc vòng M có bán kính R lăn không trượt trên mặt phẳng ngang tiến về phía vòng tròn C (hình 3). Vận tốc của tâm O1của vòng M là v. Mặt phẳng của M nằm rất sát mặt phẳngP. Gọi A là một giao điểm của hai vòng tròn khi khoảng cách giữa tâm của chúng là d Vận tốc và gia tốc của điểm A. b. Bán kính quỹ đạo và vận tốc của điểm nằm trên vòng M tại A.Bài 18. Một người chạy từ điểm O dọc theo trục Ox với vận tốc không đổi là v1. Con chó của người này lúc đầu (t = 0) ở điểm A, cách O một khoảng là L (OA Ox) bắt đầu chạy với vận tốc không đổi là v2luôn hướng vềphía chủ.