Download.vn Học tập Lớp 10

Bạn đang đọc: Bài toán thực tế quy về hệ bất phương trình bậc nhất 2 ẩn

Bài toán thực tế quy về hệ bất phương trình bậc nhất 2 ẩn Tài liệu ôn tập môn Toán lớp 10

Giới thiệu Tải về Bình luận

• 2

Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay

Bài toán thực tế quy về hệ bất phương trình bậc nhất 2 ẩn gồm 22 trang hướng dẫn giải các dạng toán thực tế quy về hệ bất phương trình bậc nhất 2 ẩn. Mời các bạn tham khảo bài viết dưới đây.

Bài toán thực tế quy về hệ bất phương trình bậc nhất 2 ẩn

4 | P a g e N g u y ễ n B á H o à n g _ Đ T : 0 9 3 6 . 4 0 7 . 3 5 3Bài toán Quy hoạch tuyến tínhA. Nội dung kiến thức.1. Bất phương trình bậc nhất hai ẩn. Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là: (1)ax by c, Ngoài dạng bất phươngtrình (1) còn có các dạng, , .ax by c ax by c ax by c     Trong đó ,,abclà các số thực, a vàb không đồng thời bằng 0, x và y là các ẩn số. Biểu diễn tập nghiệm của bất phương trình bậc nhất hai ẩn: Trong mặt phẳng toạ độ Oxy, tập hợpcác điểm có toạ độ thoả mãn bất phương trình (1) được gọi là miền nghiệm của nó. Các bước biểu diễn miền nghiệm của bất phương trình ax by c(tương tự với bất phương trình).ax by c Bước 1: Trên mặt phẳng toạ độ Oxy vẽ đường thẳng :.d ax by c Bước 2: Lấy một diểm00( ; )M x ykhông thuộc đường thẳng d. Bước 3: Tính 00ax byvà so sánh00ax byvới c. Bước 4: Kết luận: Nếu00ax by cthì nửa mặt phẳng bờ d chứa M là miền nghiệm của bất phương trình.ax by c Nếu00ax by cthì nửa mặt phẳng bờ d không chứa M là miền nghiệm của bất phương trình.ax by cVí dụ. Biểu diễn hình học tập nghiệm của bất phương trình bậc nhất hai ẩn 2 3.xyLời giảiVẽ đường thẳng:2 3.d x yLấy điểm M là gốc toạ độ O.Ta thấy Odvà2.0 3 3nên nửa mặt phẳng bờ d chứa gốc toạ độ O là miền nghiệm của bất phương trình đã cho (miền không bị tô đậm trong hình bên kể cả biên). 2. Hệ bất phương trình bậc nhất hai ẩn. Hệ bất phương trình bậc nhất hai ẩn gồm một số bất phương trình bậc nhất hai ẩn x, y mà ta phảitìm các nghiệm chung của chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ bất phươngtrình đã cho. Để biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn, ta thực hiện theo cácbước sau: Bước 1: Vẽ tất cả các đường thẳng ứng với mỗi bất phương trình trong hệ bất phương trìnhđã cho lên cùng một hệ trục toạ độ. Bước 2: Xác định miền nghiệm của từng bất phương trình trong hệ phương trình đã cho(bằng cách gạch chéo hoặc tô đậm phần không nằm trong miền nghiêm) trên hệ trục toạ độyxO(Bài toán thực tế quy về hệ bất phương trình bậc nhất 2 ẩn)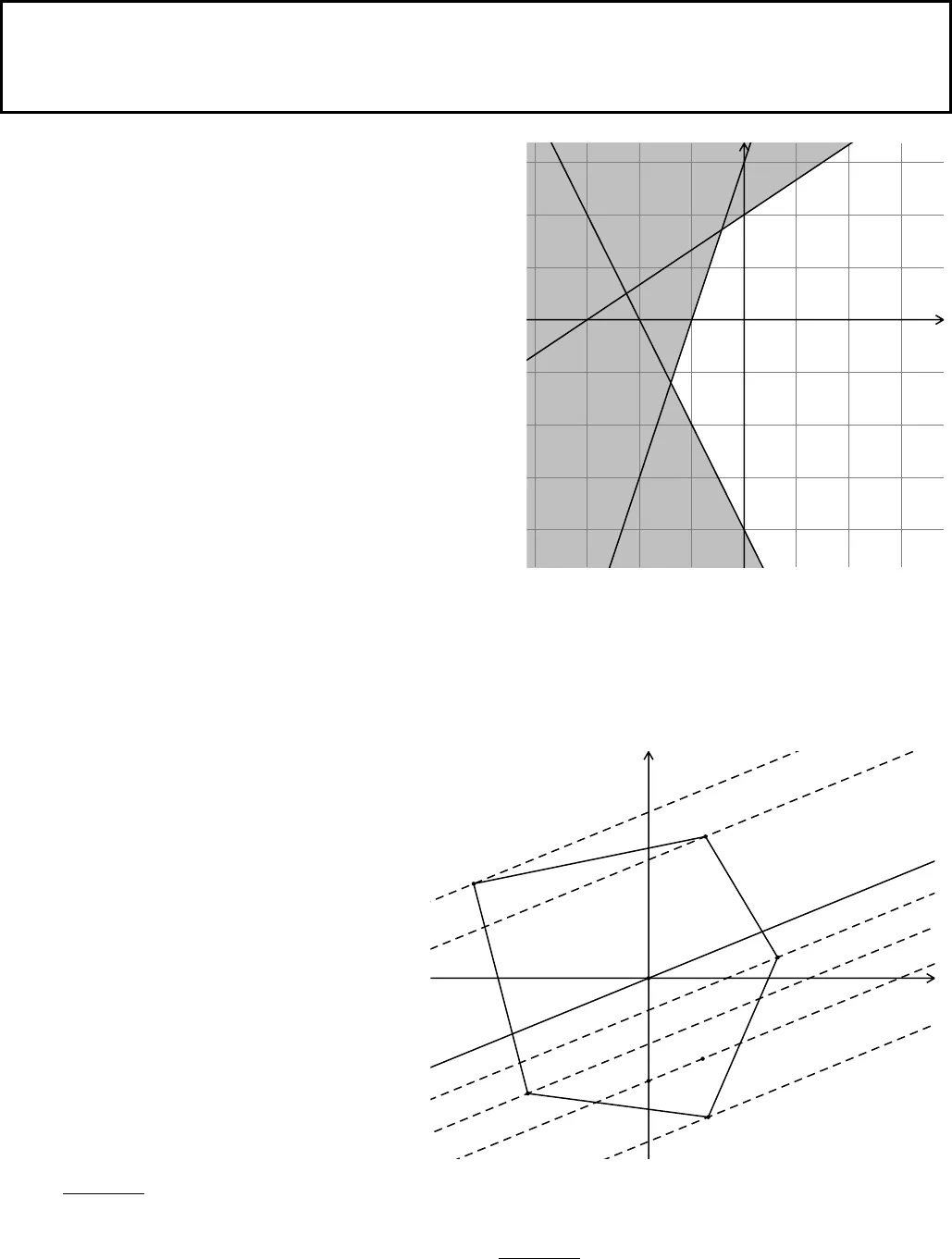5 | P a g e N g u y ễ n B á H o à n g _ Đ T : 0 9 3 6 . 4 0 7 . 3 5 3ban đầu. Phần không bị tô đậm hoặc gạch chéo chính là miền nghiệm của hệ bất phươngtrình đã cho. Ví dụ. Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn 3 3 02 3 6 0 ( ).2 4 0xyx y Ixy       Lời giảiTrước hết ta vẽ ba đường thẳng: 1( ):3 3 0;d x y  2( ): 2 3 6 0;d x y   3( ):2 4 0.d x y  Thử trực tiếp thấy (0;0)là nghiệm của cả ba bất phương trình trong hệ bất phương trình đã cho. Điều này có nghĩa là gốc toạ độ thuộc cả ba miền nghiệm của cả ba bất phương trình của hệ (I).Sau khi bỏ các miền nghiệm không thích hợp,miền không bị tô đậm trong hình bên (kể cả biên) là miền nghiệm của hệ (I).3. Bổ đề.Cho biểu thức ( , )f x y ax by, (a, b là các số thực không đồng thời bằng 0), trong đó ( ; )xylàtoạ độ của các điểm thuộc miền đa giác 12…nA A Athì giá trị lớn nhất (nhỏ nhất) của ( , )f x y(xét trên miền đa giác đã cho) đạt được tại một trong các đỉnh của miền đa giác trên. Chứng minh Tác giả sẽ chứng minh trong trườnghợp5n và0b (các trường hợp còn lại xét tương tự). Giả sử 00( ; )M x ylà một điểm đã cho thuộc miền đa giác. Qua điểm M và mỗi đỉnh của đa giác,kẻ các đường thẳng song song với đườngthẳng 0.ax byTrong các đường thẳng song song với đường thẳng 0,ax byđường thẳng qua M có phương trình 00( ) ( ) 0a x x b y y   000.ax by ax by    Đường thẳng cắt trục tung tại điểm 000; .ax byNbVì0b nên00ax bylớn nhất (nhỏ nhất) khi00ax byblớn nhất (nhỏ nhất).Quan sát hình vẽ bên ta thấy ( ; )f x ylớn nhất khi( ; )xylà toạ độ của điểm 1Avà bé nhất khi( ; )xylà toạ độ của điểm 4.Aax + by= 0A5A4A3A2A1NMyxO(d3)(d2)(d1)yxO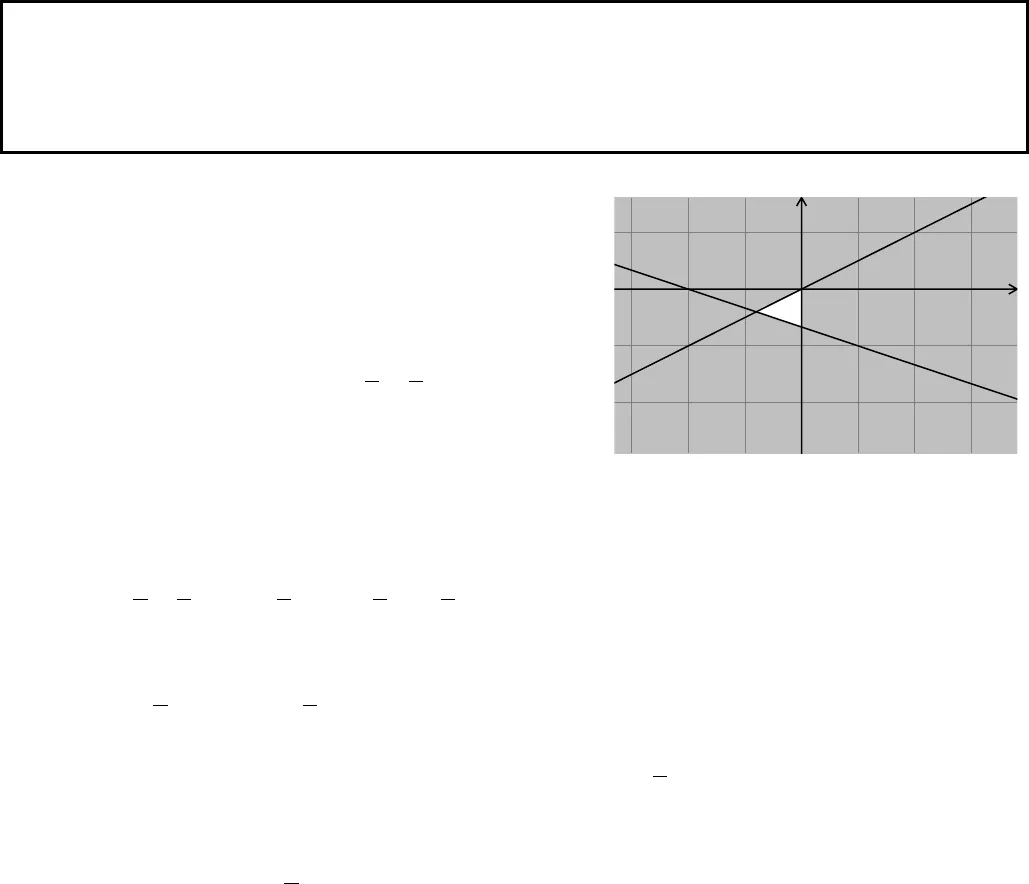6 | P a g e N g u y ễ n B á H o à n g _ Đ T : 0 9 3 6 . 4 0 7 . 3 5 3Như vậy để tìm giá trị lớn nhất (nhỏ nhât) của biểu thức ( ; )f x ytrên miền nghiệm của một hệ bất phương trình ta làm như sau:  Bước 1: Xác định miền nghiệm của hệ bất phương trình đã cho. Bước 2: Tính các giá trị của hàm số ( ; )f x yvới ( ; )xylà toạ độ các đỉnh của miền nghiệm. Bước 3: So sánh các giá trị vừa tính được với nhau, giá trị nào lớn nhất (nhỏ nhất) là giá trịlớn nhất (nhỏ nhât) của ( ; )f x ytrên miền nghiệm của hệ bất phương trình đã cho.Ví dụ. Cho hệ bất phương trình 203 2.0xyxyx  Tìm giá trị lớn nhất của hàm số( ; ) 2 3f x y x ytrênmiền nghiệm của hệ bất phương trình đã cho. Lời giảiChúng ta tìm được miền nghiệm của hệ bất phươngtrình đã cho là phần không tô đậm trong hình vẽ bên (kể cả biên).Như vậy miền nghiệm là tam giác ABC (kể cả biên). Toạ độ của điểm A là nhiệm của hệ phương trình: 2042;.3255xyAxy    Toạ độ của điểm B là nghiệm của hệ phương trình: Ta sẽ tính các giá trị của ( ; )f x yvới ( ; )xylà toạ độ của các đỉnh, , .A B O4 2 4 2 2; 2. 3. .5 5 5 5 5f                      (0;0) 2.0 3.0 0.f   220; 2.0 3. 2.33f             Suy ra giá trị lớn nhất của ( ; )f x ybằng 2 khi2( ; ) 0; .3xyVậy giá trị lớn nhất của hàm số( , ) 2 3f x y x ytrên miền nghiệm của hệ bất phương trình đã cho bằng 2 khi2( ; ) 0; .3xyLưy ý: Các kiến thức mà tác giả vừa nêu là các kiến thức cốt lõi để giải quyết các bài toán Quy hoạch tuyến tính. Tuy nhiên bài toán Quy hoạc tuyến tính lại không cho ta cụ thể hệ bất phương trình và hàm số( , )f x ynhư trong ví dụ trên mà chúng ta phải thiết lập thông qua các dữ kiện của bài toán.BAyxOxy 322 B 0;.x  03