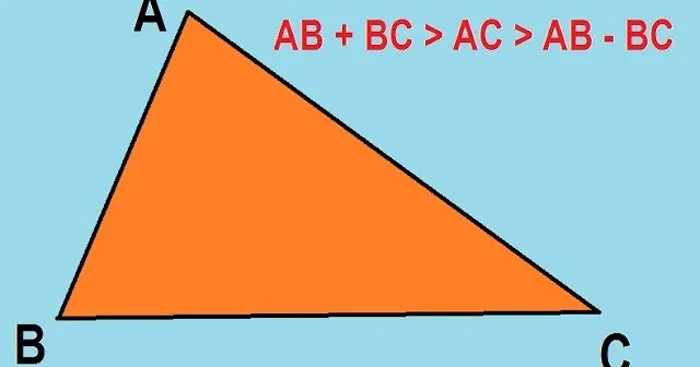
Bất đẳng thức tam giác là một trong những kiến thức quan trọng giúp các em học sinh lớp 8 giải được các dạng bài tập liên quan đến quan hệ giữa 3 cạnh trong một tam giác. Vậy bất đẳng thức tam giác là gì, các yếu tố trong tam giác có quan hệ như thế nào? Mời các em học sinh hãy cùng Download.vn theo dõi bài viết dưới đây nhé.
Bạn đang đọc: Bất đẳng thức tam giác
Thông qua tài liệu bất đẳng thức tam giác giúp học sinh củng cố, nắm vững chắc kiến thức nền tảng, vận dụng với các bài tập cơ bản để đạt được kết quả cao trong kì thi sắp tới. Vậy sau đây là nội dung chi tiết tài liệu, mời các bạn cùng theo dõi tại đây.
Bất đẳng thức tam giác
1. Bất đẳng thức tam giác là gì?
Trong toán học, bất đẳng thức tam giác là một định lý phát biểu rằng trong một tam giác, chiều dài của một cạnh phải nhỏ hơn tổng, nhưng lớn hơn hiệu của hai cạnh còn lại .
Trong một tam giác bất kỳ, tổng độ dài hai cạnh bao giờ cũng lớn hơn độ dài cạnh còn lại
– Xét tam giác ABC ta có:
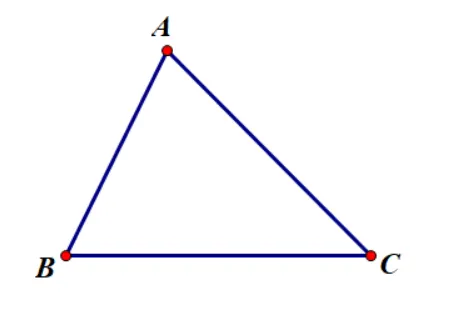
AB + AC > BC
AB + BC > AC
AC + BC > AB
2. Bài tập bất đẳng thức
Ví dụ 1: Cho a, b, c là độ dài ba cạnh của 1 tam giác. Chứng minh rằng
Gợi ý đáp án
Ta có
Tương tự ta có:
Cộng vế theo vế ta được
Vậy
Ví dụ 2: Cho a, b, c > 0. Chứng minh rằng:
Gợi ý đáp án
Ta có :
Tương tự ta có:
Cộng theo vế ta được:
Ví dụ 3: Cho tam giác ABC có độ dài ba cạnh là a, b,c chu vi là 2p. Chứng minh rằng:
Gợi ý đáp án
Ta có
Chứng minh tương tự ta có:
và
Nhân theo vế ta được:
Ví dụ 4: Cho a + b + c = 1. Chứng minh rằng:
Gợi ý đáp án
Đặt .
Cộng theo vế ta được
Mà . Thay vào (1) ta được
(đpcm)
Ví dụ 5: Cho a, b,c > 0 thỏa mãn .
Tìm GTLN của
Gợi ý đáp án
Ta có:
Áp dụng BĐT Cauchy – Schawzr ta có:
Mà thay vào (1) ta được