Download.vn Học tập Lớp 12
Bạn đang đọc: Bộ đề kiểm tra 1 tiết chương I Giải tích lớp 12
Bộ đề kiểm tra 1 tiết chương I Giải tích lớp 12 4 Đề kiểm tra 45 phút Giải tích lớp 12 chương I
Giới thiệu Tải về Bình luận
- 1
Mua tài khoản Download Pro để trải nghiệm website Download.vn KHÔNG quảng cáo & tải File cực nhanh chỉ từ 79.000đ. Tìm hiểu thêm Mua ngay
Download.vn xin giới thiệu đến quý thầy cô giáo, cùng các bạn học sinh lớp 12 Bộ đề kiểm tra 1 tiết chương I Giải tích lớp 12.
Bộ đề kiểm tra 1 tiết chương I Giải tích lớp 12 là tài liệu tham khảo hữu ích, gồm 6 đề có đáp án đi kèm giúp cho quý thầy cô giáo, các bạn học sinh có thêm nhiều tư liệu ôn tập phục vụ cho việc ra đề và ôn tập nhằm chuẩn bị cho bài thi cuối học kỳ 1 sắp tới. Nội dung chi tiết mời các bạn cùng tham khảo và tải tài liệu tại đây.
Bộ đề kiểm tra 1 tiết chương I Giải tích lớp 12
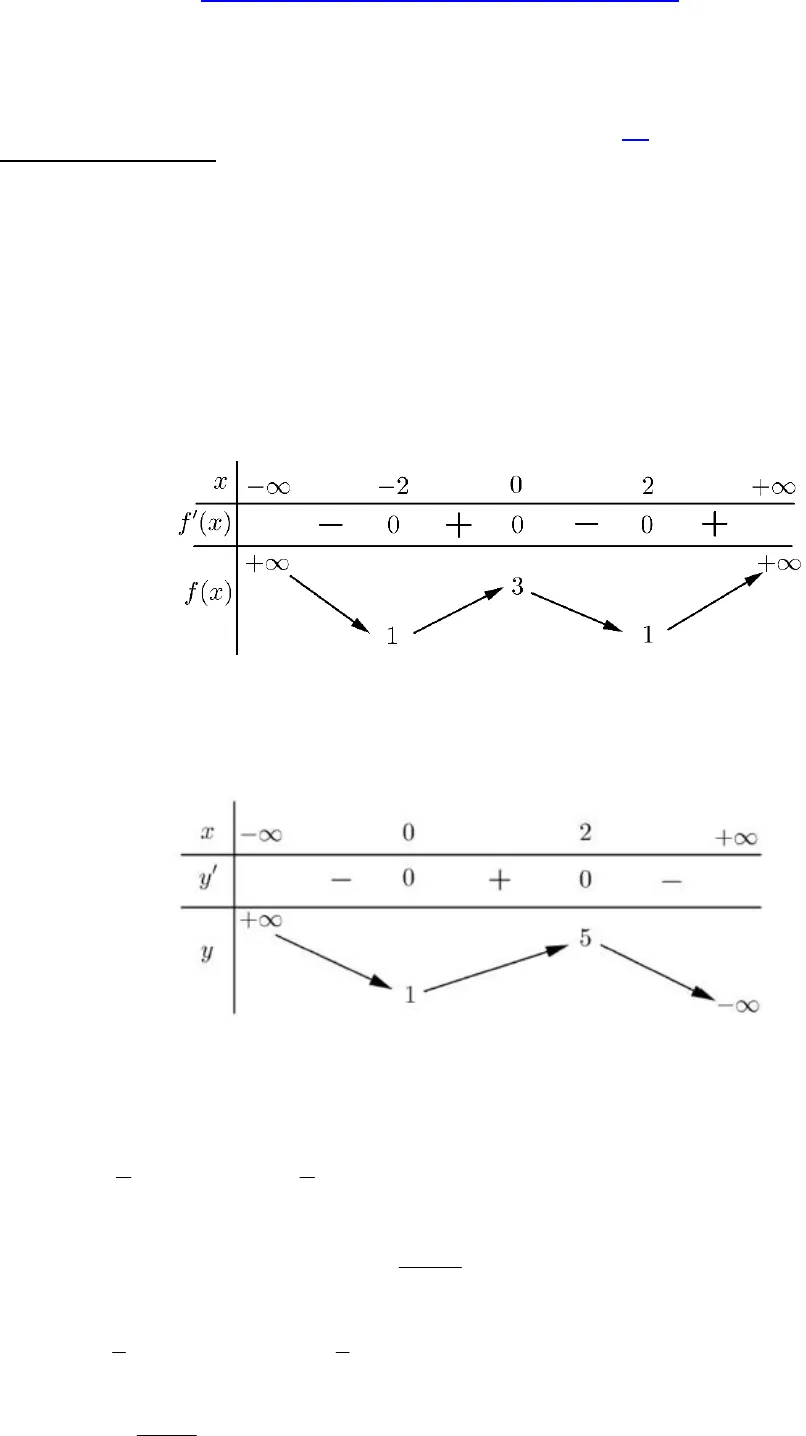KIỂM TRA 1 TIẾT CHƯƠNG I GIẢI TÍCH 12ĐỀ 1SỞ GD&ĐT …………….TRƯỜNG ………..Đề chính thức(Đề kiểm tra gồm 04 trang)ĐỀ KIỂM TRA 1 TIẾTMôn: Giải tích 12 – THPTNăm học 2019 – 2020Thời gian làm bài: 45 phút(Không kể thời gian giao đề)I. TRẮC NGHIỆM KHÁCH QUAN (8,0 điểm).Câu 1. Cho hàm số f xcó bảng biến thiên như sau:Hàm số đã cho nghịch biến trên khoảng nào dưới đây?A. 2;0. B.( ;1)+ ¥. C. 0;2. D.(3;1).Câu 2. Cho hàm số( )y f x=có bảng biến thiên như sauGiá trị cực đại của hàm số đã cho bằngA.1. B.2. C.0. D.5.Câu 3. Hàm số42 1y x đồng biến trên khoảng nào?A.1;2 . B.1;2 . C. 0;. D.( ;0).Câu 4. Tìm giá trị lớn nhất M của hàm số3 13xyx-=-trên đoạn[ ]0;2A.13M . B.13M . C.5M . D.5M .Câu 5. Hàm số2 31xyxcó bao nhiêu điểm cực trị?A.3. B.0. C.2. D.1.
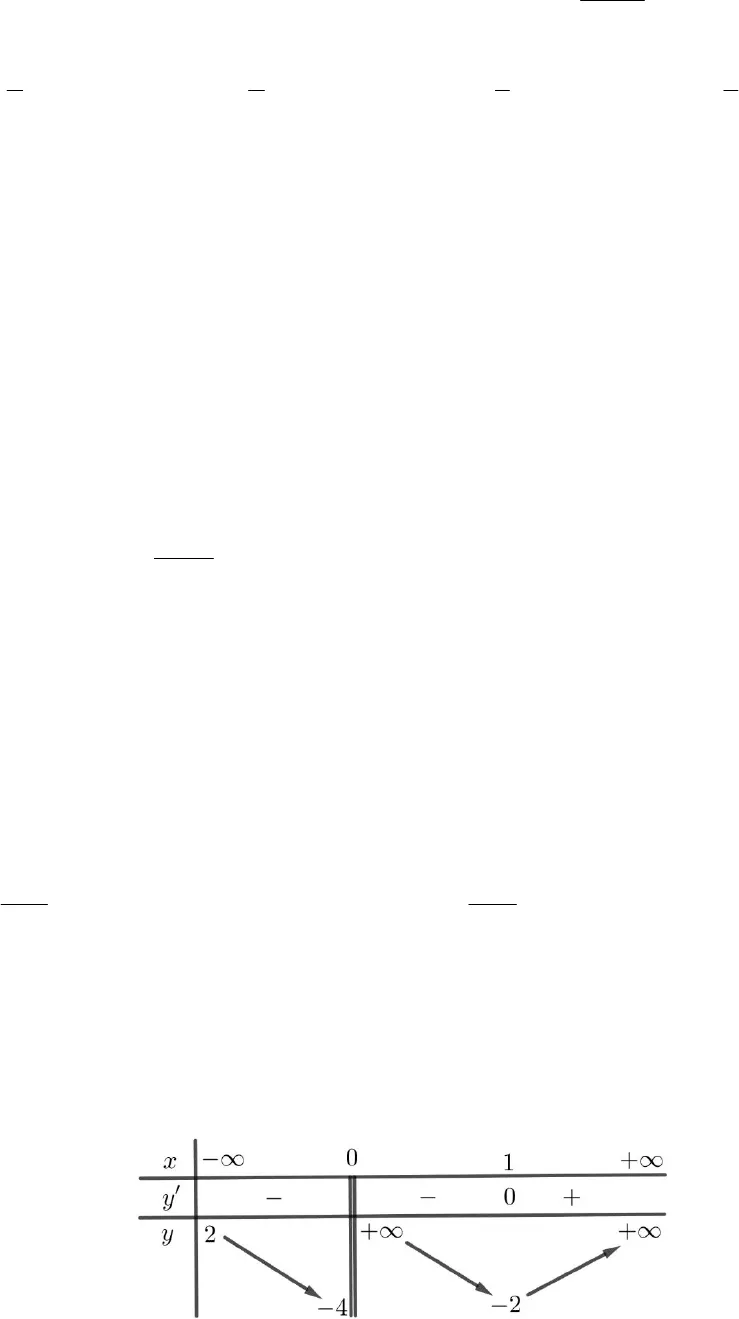Câu 6. Tìm phương trình các đường tiệm cận đứng của đồ thị hàm số2 13 1xyx-=+A.23x =. B.23y =. C.13x = –. D.13y = –.Câu 7. Giá trị lớn nhất của hàm số3( ) 3 2f x x x trên đoạn[ 3;3]bằngA.16. B.20. C.0. D.4.Câu 8. Cho hàm số( )y f x, có đạo hàm2′( ) 1,f x x x R . Mệnh đề nào dưới đây đúng?A. Hàm số đồng biến trên khoảng(1; )+ ¥.B. Hàm số nghịch biến trên khoảng( ; )– ¥ + ¥.C. Hàm số đồng biến trên khoảng( ; )– ¥ + ¥.D. Hàm số nghịch biến trên các khoảng( )1;1–.Câu 9. Cho đồ thị hàm số2 31xyx . Mệnh đề nào sau đây đúng?A. Đồ thị hàm số có đường tiệm cận đứng là1x .B. Đồ thị hàm số có đường tiệm cận ngang là2x .C. Đồ thị hàm số có đường tiệm cận đứng là1y .D. Đồ thị hàm số có đường tiệm cận ngang là2y .Câu 10. Hàm số nào dưới đây đồng biến trên khoảng ; ?A.13xyx. B.3y x x . C.12xyx. D.33y x x .Câu 11. Tìm giá trị cực tiểu của đồ thị hàm số3 22 3 2y x x= – –.A.3CTy = –. B.2CTy = –. C.0CTy =. D.1CTy =.Câu 12. Cho hàm số y f xcó bảng biến thiên như sau:Số tiệm cận ngang của đồ thị hàm số đã cho làA.4.. B.1.. C.3.. D.2..
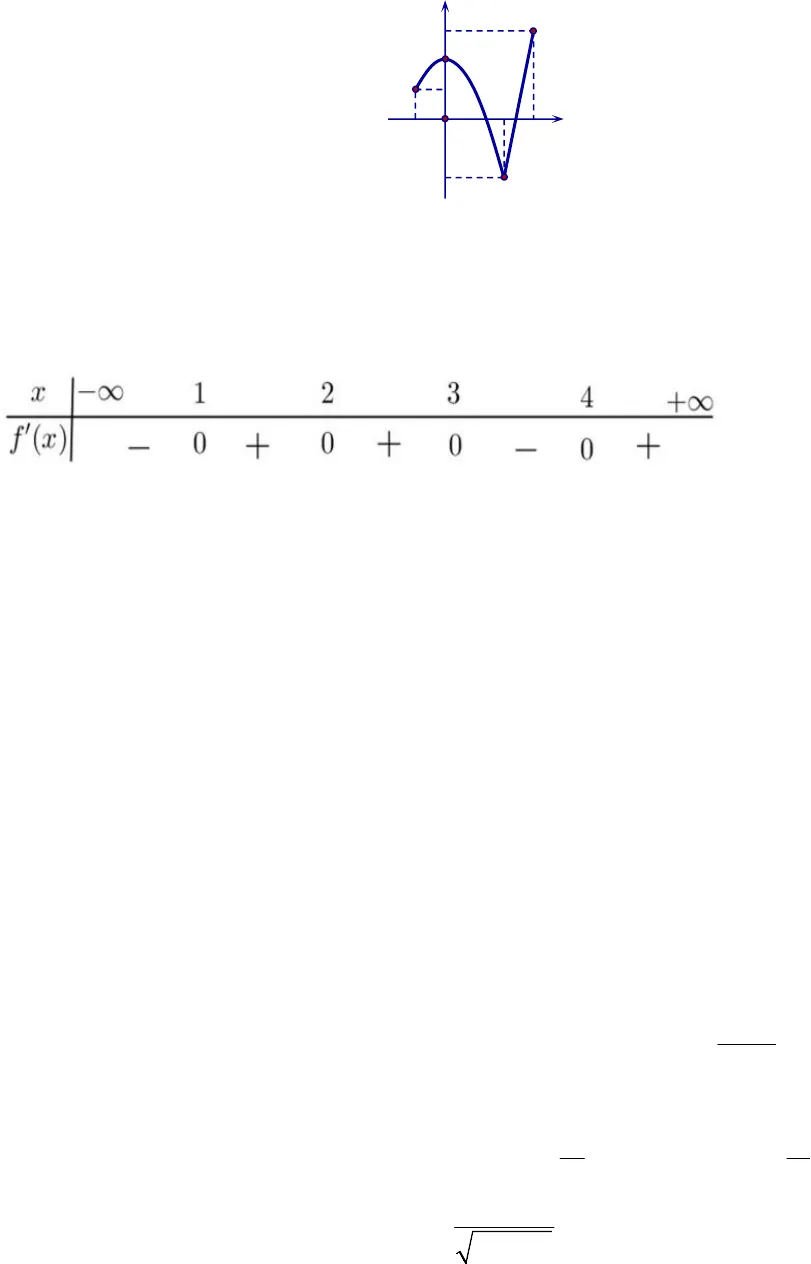Câu 13. Cho hàm số y f xliên tục trên đoạn 1;3và có đồ thị như hình bên. GọiMvàmlần lượtlà giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn 1;3. Giá trị củaM mbằngO2231123yxA.0. B.1. C.4. D.5.Câu 14. Cho hàm số( )f xcó bảng xét của đạo hàm như sau:Số điểm cực trị của hàm số đã cho làA.3. B.2. C.4. D.1.Câu 15. Cho hàm số( )y f x=cólim ( ) 1xf x® + ¥=vàlim ( ) 1xf x® – ¥= -. Khẳng định nào sau đây là khẳngđịnh đúng?A. Đồ thị hàm số đã cho không có đường tiệm cận ngang.B. Đồ thị hàm số đã cho có đúng một đường tiệm cận ngang.C. Đồ thị hàm số đã cho có hai đường tiệm cận ngang là các đường thẳng1y =và1y = –.D. Đồ thị hàm số đã cho có hai đường tiệm cận ngang là các đường thẳng1x =và1x = –.Câu 16. Tính tổng giá trị cực đại và giá trị cực tiểu của hàm số3 23 2y x x= – +.A. 3. B. 2. C. 1. D. 0.Câu 17. GọiM,mlần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số252xyxtrên 2;1. Tính2T M m .A.14T . B.10T . C.212T . D.132T .Câu 18. Đường tiệm cận ngang của đồ thị hàm số22 14 3xyx-=+A.1y =. B.2; 2y y= = –. C.2y =. D.1; 1y y= – =.Câu 19. Cho hàm số f xcó đạo hàm2 3′( ) ( 1)( 2) ( 3)f x x x x ,x . Số điểm cực trị của hàm sốđã cho là