SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
|
ĐỀ THI HỌC KỲ I NĂM HỌC 2012- 2013
|
Bài 1 (2,5 điểm)
Cho hàm số
1. Khảo sát sự biến thiên và vẽ đồ thị (H) của hàm số (1)
2. Tìm m để đường thẳng y = mx – 1 cắt đồ thị (H) tại hai điểm phân biệt A, B sao cho trung điểm của đoạn thẳng AB thuộc đường thẳng y = x – 1.
Bài 2 (2 điểm)
1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số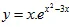 
trên đoạn [-1; 1]
2. Cho hàm số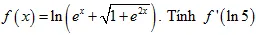 
Bài 3 (2 điểm)
1. Giải phương trình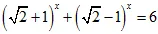 
2. Cho phương trình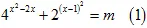 
, với m là tham số.
a) Giải phương trình (1) khi m = 3
b) Tìm m để phương trình (1) có nghiệm duy nhất.
Bài 4 (3,5 điểm)
Cho hình chóp S.ABC có mặt phẳng (SAB) vuông góc mặt phẳng (ABC), SA = SB = a, góc ASB = 120o, mặt đáy ABC là tam giác vuông tại C, BC = a.
1. Tính thể tích khối chóp S.ABC
2. Tính khoảng cách từ điểm B tới mặt phẳng (SAC)
3. Gọi C’ là trung điểm của cạnh SC. Xác định tâm và tính bán kính mặt cầu ngoại tiếp hình chóp C’.ABC
Download tài liệu để xem thêm chi tiết
