Toán lớp 8 tập 1 trang 82, 83, 84, 85, 86, 87 Chân trời sáng tạo là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 8 tham khảo.
Bạn đang đọc: Toán 8 Bài 5: Hình chữ nhật – Hình vuông
Giải Toán 8 Chân trời sáng tạo Bài 1 Hình chữ nhật – Hình vuông được biên soạn đầy đủ, chi tiết trả lời các câu hỏi phần bài tập cuối bài trang 86, 87. Qua đó giúp các bạn học sinh có thể so sánh với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết Toán lớp 8 tập 1 chương III Bài 1 Hình chữ nhật – Hình vuông Chân trời sáng tạo, mời các bạn cùng theo dõi tại đây.
Giải Toán 8 Bài 5: Hình chữ nhật – Hình vuông
Bài tập 1
Cho hình 14. Tìm x
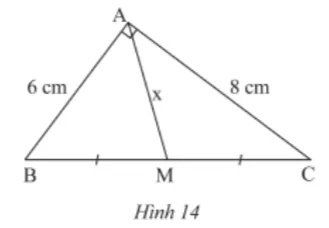
Gợi ý đáp án
ΔABC vuông tại A có: (định lí Pytago)
⇒ hay BC = 10 (cm)
Mà AM= (đường trung tuyến ứng với cạnh huyền)
Nên AM= x 10=5(cm)
Vậy x=5cm
Bài tập 2
Cho hình 15. Vẽ thêm điểm P để tứ giác MNPQ là hình chữ nhật.
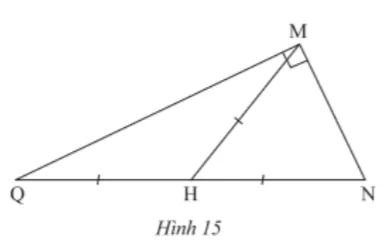
Gợi ý đáp án
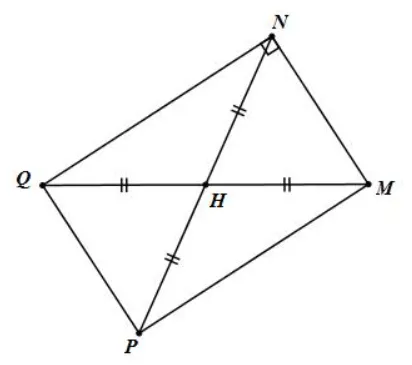
Cách vẽ:
Trên tia đối của tia HM lấy điểm P sao cho HP=HM
Chứng minh:
Tứ giác MNQP có QN và MP cắt nhau tại trung điểm của mỗi đường.
Do đó tứ giác MNQP là hình bình hành (dấu hiệu nhận biết)
Mặt khác (gt) ⇒ Tứ giác MNQP là hình chữ nhật (dấu hiệu nhận biết).
Bài tập 3
Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm dối xứng với H qua I. Gọi M, N lần lượt là trung điểm của HC, CE. Các đường thẳng AM, AN cắt HE tại G và K.
a) Chứng minh tứ giác AHCE là hình chữ nhật.
b) Chứng minh HG = GK = KE.
Gợi ý đáp án
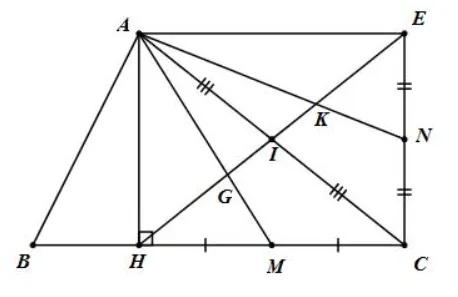
a) Tứ giác AHCE có hai đường chéo AC và HE cắt nhau tại I (gt)
I là trung điểm của AC (gt);
Và I là trung điểm của HE (E đối xứng với H qua I)
Do đó tứ giác AHCE là hình bình hành.
Mà (AH là đường cao của tam giác ABC)
Vậy tứ giác AHCE là hình chữ nhật.
b) MAHC có: HI là đường trung tuyến (I là trung điểm của AC)
Và AM là đường trung tuyến (M là trung điểm của HC)
Mà HI cắt AM tại G (gt)
Do đó G là trọng tâm của tam giác AHC ⇒ (1)
ΔAEC có hai đường trung tuyến AN và EI cắt nhau tại K.
⇒K là trọng tâm của tam giác AEC ⇒ (2)
HI=IE (E đối xứng với H qua I) (3)
Từ (1), (2) và (3) suy ra HG=KE=
Ta có:
Bài tập 4
Cho tam giác ABC vuông tại A (AB
a) Chứng minh rằng tứ giác AEDF là hình chữ nhật.
b) Chứng minh rằng tứ giác BFED là hình bình hành.
Gợi ý đáp án
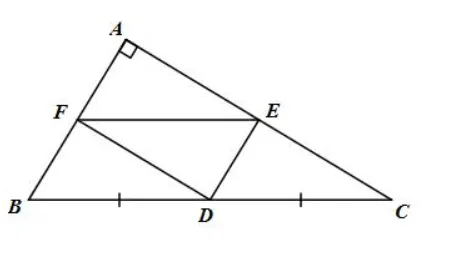
a) Tứ giác AEDF có:
AE // DF (AC // FD, E∈AC)
AF // DE (AB // DE, F∈AB)
⇒AEDF là hình bình hành.
Mà (ΔABC vuông tại A)
Nên AEDF là hình chữ nhật.
b) ΔABC có D là trung điểm của BC và FD // AC ⇒F là trung điểm của AB.
ΔABC có D là trung điểm của BC và DE // AB ⇒E là trung điểm của AC
⇒ EFlà đường trung bình của tam giác ABC
⇒ EF//BC và EF=
Lại có BD= (Vì D là trung điểm của BC)
⇒ EF//BD và EF=BD
Vậy tứ giác BFED là hình bình hành (dấu hiệu nhận biết).
Bài tập 5
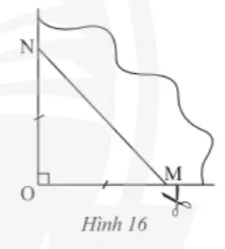
Lấy một tờ giấy gấp làm tư để có một góc vuông như trong Hình 16, dùng kéo cắt theo đường MN sao cho OM = ON. Mở phần giấy cắt được ra ta được một tứ giác.
Tứ giác đó là hình gì? Giải thích kết luận của em.
Gợi ý đáp án
– Tứ giác nhận được theo nhát cắt của MN là hình thoi vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau.
– Nếu có thêm OM = ON thì hình thoi nhận được có hai đường chéo bằng nhau nên là hình vuông.
